充分发展流的意义是什么?
-
@李东岳 李老师,看了boundaryFoam解析,也提到了充分发展湍流特性,但我还是没太明白充分发展湍流为何是这种特性,主要疑问如下:

- 对于充分发展的槽道湍流,瞬时的$\frac{\partial U(t)}{\partial x}$应该不等于0(因为流场为湍流,同个高度速度都有脉动值),这里的特征$\frac{\partial U}{\partial x}=0$中的速度是否指平均速度?
- 对于不可压缩流体,入口只施加平均风剖面速度(比如$U_x(z)$用对数率剖面,$U_y(z)=0$,$U_z(z)=0$)。之前算过这种工况的LES,结果是整个流场平均均按照自保持发展,基本没改变。对应的数学描述为:$\frac{\partial U_x(t)}{\partial x}=0$,$\frac{\partial p}{\partial x}=很小值$。另外再根据知乎帖子,这种平均风流动是否可称为充分发展剪切层流?
- 之前对湍流充分发展概念不理解,然后自己做了个猜想。把湍流发展类比于高中物理中的经典两个小球非弹性碰撞问题,湍流发展发生碰撞,碰撞就会产生力,力改变速度,接着发展趋向于使得两个碰撞物体平均速度(但瞬时速度不同)变为一致,
最后脉动速度以相同平均速度向前发展形成充分发展湍流。
(1)最后脉动速度以相同平均速度向前发展形成充分发展湍流,这正对应于泰勒冻结假设:湍流在顺风向以平均速度移动,且湍流在运动过程中没有发生形态的显著变化。
(2)针对上面阐述,很容易产生疑问:充分发展时,湍流微元体在同个高度不同位置的速度不同,但为何都只是按照平均速度在输运?脉动速度对输运不起作用吗?针对这个问题尝试做的解释如下:
①x向的动量如下,大写字母表示合速度,小写表示脉动速度,脉动速度均值等于0
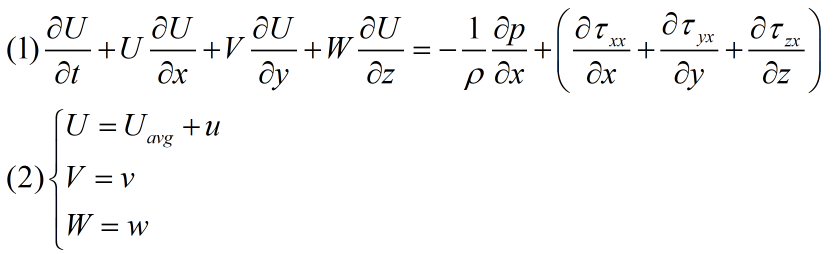
②将式(2)代入式(1),并以移项得到式(3):
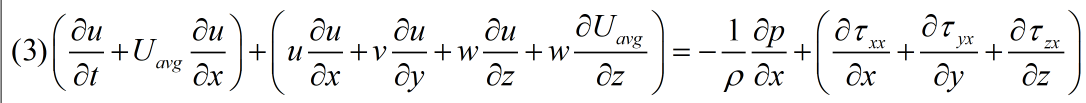
③当湍流充分发展,微元体受到的合力应该等于0(不引起速度改变),即式(3)右边项等于0。根据泰勒冻结假设,湍流形态没显著变化,对应剪切应力不变,因此充分发展的湍流场:$\frac{\partial p}{\partial x}=常数$,并由于空气的粘性很小,对应剪切力很小,因此$\frac{\partial p}{\partial x}=很小值$。这对应了风工程中研究大气边界层湍流风场生成方法,为何要求空风洞中的压力接近于很小值才合理。
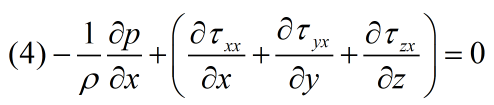
④因为充分发展流场按照泰勒冻结假设发展,这正对应于式(3)左边括号第一项等于0,即脉动速度物理量以平均速度输运:
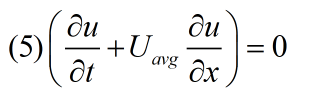
⑤那么最后式(3)左边括号第2项也应等于0。该项等于0,说明了不同脉动速度的输运会相互抵消,这解释了为何充分发展时,不同位置的瞬时速度不同,但都以平均速度输运。
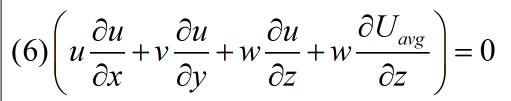
- 以上是困扰我很久的问题,针对自己疑问做的猜想,不知道合不合理,请各位大佬批评指正。总结一下猜想:三维充分发展湍流的特征是按照泰勒冻结假设方式发展,流场中压力梯度为很小值;瞬时脉动速度梯度不等于0:$\frac{\partial u}{\partial x}\neq 0, \frac{\partial u}{\partial y}\neq 0, \frac{\partial u}{\partial z}\neq 0 $

