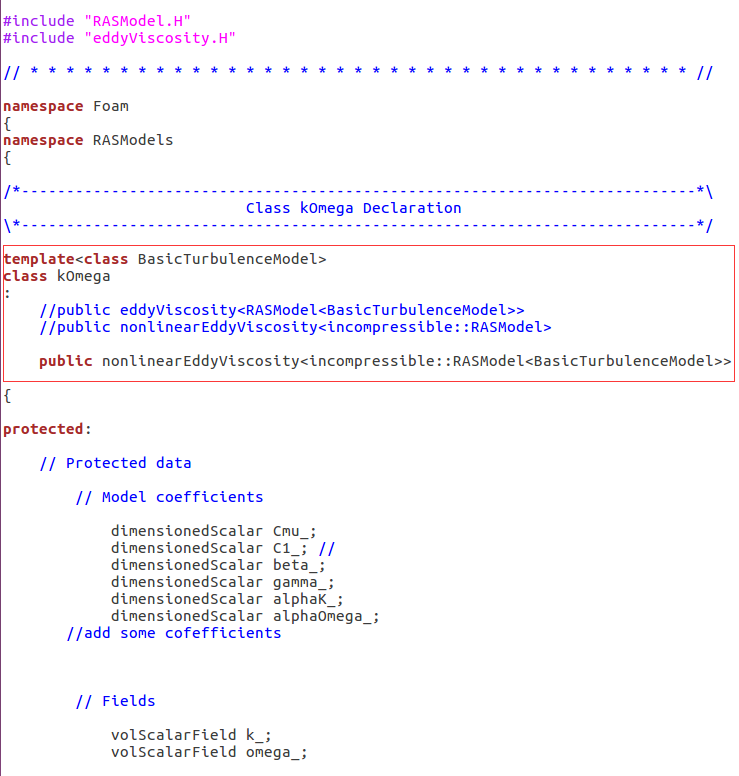
关于修改湍流模型中非线性雷诺应力项的问题
-
@李东岳 谢谢老师对我问题的指导,理解了针对“动量方程”雷诺应力项的修改就是通过修改linearViscousStress.C。
我先介绍下我的研究方向:模拟三层液态金属组成的电池的不稳定性,随着电压增加时三层流体会发生不稳定性即湍流,目前组里采用DNS计算消耗计算资源太大,所以我需要采用湍流模型来尝试一下这个发生过程,我采用了基于磁流体修改后的K-omega模型,其需要加入磁动能源项与各项异性的雷诺应力,以下是我需要修改的非线性雷诺应力项:
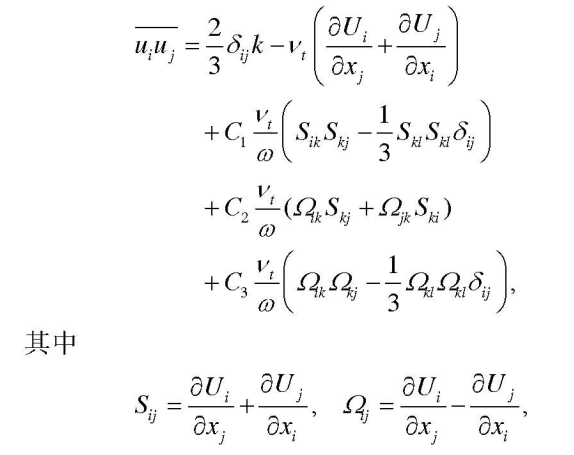
我的问题是:雷诺应力也包含在kOmega.H中如下:tmp<volTensorField> tgradU = fvc::grad(U); volScalarField G ( this->GName(), nut*(tgradU() && dev(twoSymm(tgradU()))) ); tgradU.clear(); tmp<fvScalarMatrix> omegaEqn ( fvm::ddt(alpha, rho, omega_) + fvm::div(alphaRhoPhi, omega_) - fvm::laplacian(alpha*rho*DomegaEff(), omega_) == gamma_*alpha*rho*G*omega_/k_ - fvm::SuSp(((2.0/3.0)*gamma_)*alpha*rho*divU, omega_) - fvm::Sp(beta_*alpha*rho*omega_, omega_) + fvOptions(alpha, rho, omega_) + fvm::SuSp(Comg_*S/k_, omega_) );其中G中包含线性雷诺应力,针对这个非线性雷诺应力是不是我需要同时:
1、修改动量方程中的,即通过修改linearViscousStress.C;
2、修改kOmega模型中的,即也要修改上面的G。初学openfoam见识浅薄,希望各位老师和同学能不吝赐教。
-
@chen_hao 在 关于修改湍流模型中非线性雷诺应力项的问题 中说:
您所指的加上雷诺应力非线性部分就是UEqn.H中turbulence->divDevRhoReff(rho, U)项的修改对吗?
不是,不需要修改这个函数,你仔细看看 ShihQuadraticKE 这个模型的继承关系,它继承的是 nonLinearEddyViscousity 类。这个类计算雷诺应力的方式不一样,除了线性项还有一个 nonLinearStress 项。你只要按照这个框架去写,把你的非线性项赋值给 nonLinearStress 就行了。

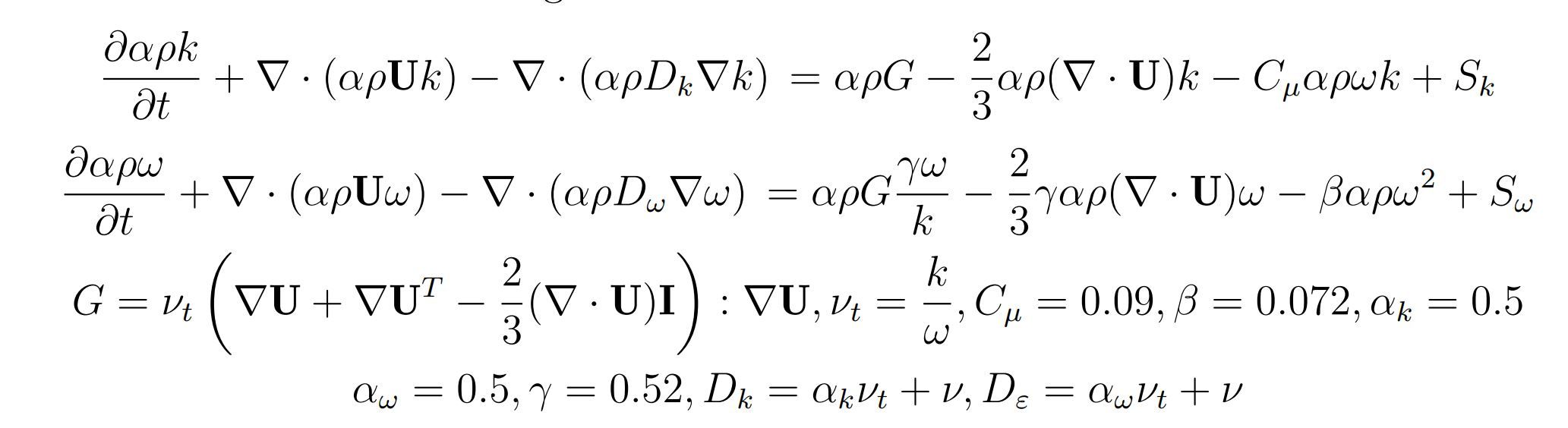
![1d4c6455-e7c6-4745-adca-6daf38318f29-H[]@OX2Z%XH)C}(8LJMOR1Q.png](/assets/uploads/files/1655455976275-1d4c6455-e7c6-4745-adca-6daf38318f29-h-ox2z-xh-c-8ljmor1q.png)

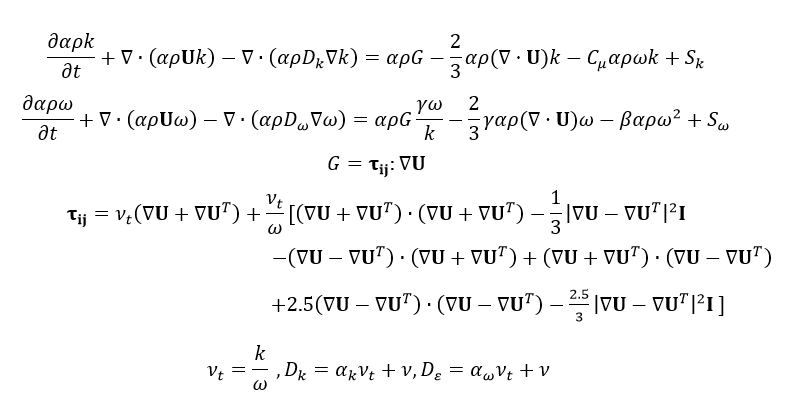
![431a9ef8-7ab7-4486-909b-7e8b4d3848ad-L[OCC5NV(U5VNABTKSCMH]P.png](/assets/uploads/files/1655698130909-431a9ef8-7ab7-4486-909b-7e8b4d3848ad-l-occ5nv-u5vnabtkscmh-p.png)