pisoFoam计算的U,求div(U)结果为何不是严格等于0
-
参考李老师的icoFoam解析,PISO算法在根据式(32)计算得到$p^*$,再根据式(31)得到 $\mathbf{U}^{**}$,此时的$\mathbf{U}^{**}$应该满足零散度条件:$\nabla\cdot{\mathbf{U}^{**} }=0$。
但是在计算of2206自带一个算例:Decay of homogeneous isotropic turbulence,用postProcess -func "div(U)"输出不同时刻的div(U),并求最大值、最小值、均值和标准差,发现0.28,0.66 s的div(U)结果并不是一个很小的值。尝试设置tolerance=1e-10,结果也是基本一样;更改nCorrectors=5,结果也是一样。
问题:是否理论上$\nabla\cdot\mathbf{U}^{**} =0$,但数值误差影响导致结果不等于0?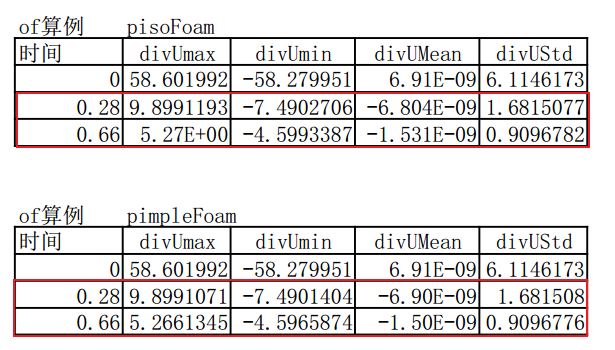

-
@李东岳 李老师,发现一个问题。
- 如果用
myphi = fvc::flux(U)计算,然后求div(myphi)和div(U)结果基本是一致的。 - 问题出现在PISO算法中,
pEqn.H采用phi = phiHbyA - pEqn.flux()得到phi,U通过U = HbyA - rAU*fvc::grad(p)得到。若接着计算myphi = fvc::flux(U),此时myphi与phi结果不一致。 - 具体算例结果:
(1)编译了mypisoFoam,参考createPhi.H创建myphi,pEqn.H中最后增加myphi = fvc::flux(U);,计算输出phi,myphi,U,接着算
postProcess -func "div(U)" postProcess -func "div(phi)" postProcess -func "div(myphi)"(2)取部分结果展示:
①phi结果internalField nonuniform List<scalar> 774144 ( 9.2226869e-06 -1.2808218e-05 3.6560601e-06 -1.834312e-06 -1.5738475e-05 -5.2343047e-06 -3.6611478e-06
②
myphi结果internalField nonuniform List<scalar> 774144 ( 9.0864005e-06 -1.2188111e-05 3.3814109e-06 -1.946668e-06 -1.5267671e-05 -5.1722677e-06 -3.3374742e-06
③
div(U)结果internalField nonuniform List<scalar> 262144 ( -0.40218979 0.59941437 0.85901197 -2.6335161 -0.55062117 -0.53919284 2.4044185 1.1295023 -1.7101542
④
div(myphi)结果internalField nonuniform List<scalar> 262144 ( -0.40218974 0.59941339 0.85901118 -2.6335163 -0.55062104 -0.53919262 2.404419 1.1295015 -1.710154
⑤
div(phi)结果internalField nonuniform List<scalar> 262144 ( -3.1704547e-08 -6.3409098e-07 6.3409098e-07 8.9515991e-16 -2.1136366e-07 3.3818186e-07 1.0568183e-07 -4.2272732e-07 -5.7068188e-07- 结果分析:
①phi与myphi的值看起来差别不大。
②但div(phi)结果基本等于0;div(U)和div(myphi)结果一样,但不等于0。
问题:既然phi定义为fvc::flux(U),为何of中最后输出phi不用fvc::flux(U),而是用了phi = phiHbyA - pEqn.flux()?此时计算的通量myphi=fvc::flux(U),实际上也没满足div(myphi)=0
- 如果用
-
@coolhhh 在 pisoFoam计算的U,求div(U)结果为何不是严格等于0 中说:
为何of中最后输出phi不用fvc::flux(U),而是用了phi = phiHbyA - pEqn.flux()?
fvScalarMatrix pEqn ( fvm::laplacian(rAU, p) == fvc::div(phiHbyA) ); pEqn.setReference(pRefCell, pRefValue); pEqn.solve(); phi = phiHbyA - pEqn.flux();上面这几行代码里面,
pEqn实际上是建立在sum(phi)= sum(phiHbyA - pEqn.flux())=0,也就是说,在sum(phi)= sum(phiHbyA - pEqn.flux())=0的时候,才有fvm::laplacian(rAU, p) == fvc::div(phiHbyA)这个形式。所以求解fvm::laplacian(rAU, p) == fvc::div(phiHbyA),sum(phi)= sum(phiHbyA - pEqn.flux())=0。 -
李老师,我做了简单的对比:
-
下面计算的
div(U)与div(phi)结果基本相等,区别是小数点后五六位
①直接求div(U)
②已知U->phi = fvc::flux(U)->div(phi) -
接着对比
reconstruct(phi)。编译mypisoFoam,把pEqn.H中计算U修改为
U = fvc::reconstruct(phi); // U = HbyA - rAU*fvc::grad(p);同样计算计算of2206自带一个算例:Decay of homogeneous isotropic turbulence,模拟结果:
(1)对比div(U)与div(phi)的均值和标准差。采用reconstruct(phi),得到的div(U)的均值和标准差要小一点。这里有个注意点是,of计算的div(phi),基本数值都很小,但会有一个比较大的数,下面的计算结果是剔除了这个最大数的计算结果。
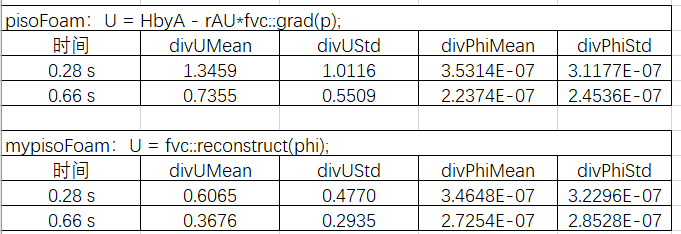
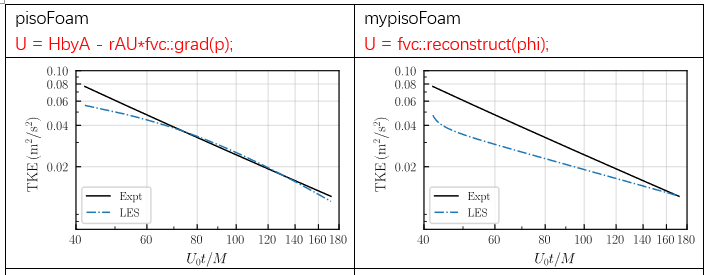
(2)对比湍流特性。可以看出
reconstruct(phi)结果要更差,还是原本of的U = HbyA - rAU*fvc::grad(p)计算准确
-
-
谢谢李老师,文章已经发表了,只是好奇做个对比。在想的问题是,一直以来各种湍流生成方法都在追求实现生成零散度的湍流场
U,我们直接构造的是0时刻的U,而不是phi。根据测试结果看,如果严格让
div(U)=0, 此时U -> phi = fvc::flux(U) -> div(phi)得到的div(phi)也基本等于0。但这种情况下0时刻的湍流特性会变化的比较大,结果会变差。of在后面时间步计算输出的
U实际上不满足div(U)=0,所以想法是0时刻提供的初始U也不需要强制要求div(U)=0,这样得到的结果可能才是更合理的。 -
C coolhhh 被引用 于这个主题
-
C coolhhh 被引用 于这个主题

