并行效率疑问
-
简单说一下case的情况:
三维圆柱绕流,pisoFoam, incompressible solver, LES dynamic k equation, Re 10^5, 3千万结构网格。
为了加速运算,又使用了576核试算,infinband, 24cores/node, 32 Gb mem /node。预计比288核那个case要快,结果挺意外的:
288 core 运行到0.014 second 的时候 clockTime 631 s
Time = 0.014 Courant Number mean: 0.0209991 max: 0.860686 DILUPBiCG: Solving for Ux, Initial residual = 0.000686338, Final residual = 5.79235e-09, No Iterations 3 DILUPBiCG: Solving for Uy, Initial residual = 0.000616596, Final residual = 2.39462e-07, No Iterations 2 DILUPBiCG: Solving for Uz, Initial residual = 0.25073, Final residual = 2.22608e-08, No Iterations 3 GAMG: Solving for p, Initial residual = 0.0951268, Final residual = 0.00450444, No Iterations 2 time step continuity errors : sum local = 3.43222e-08, global = 3.79731e-10, cumulative = -1.1601e-09 GAMG: Solving for p, Initial residual = 0.00459438, Final residual = 0.000221683, No Iterations 11 time step continuity errors : sum local = 1.67411e-09, global = -1.41906e-10, cumulative = -1.302e-09 GAMG: Solving for p, Initial residual = 0.000220326, Final residual = 9.99438e-08, No Iterations 59 time step continuity errors : sum local = 7.78239e-13, global = -1.40881e-16, cumulative = -1.302e-09 DILUPBiCG: Solving for k, Initial residual = 0.0347117, Final residual = 7.93887e-08, No Iterations 2 bounding k, min: -1.42701e-10 max: 6.66159e-05 average: 7.69531e-09 ExecutionTime = 627.61 s ClockTime = 631 s576 核 ClockTime = 2914 s
Time = 0.014 Courant Number mean: 0.0209908 max: 0.853335 DILUPBiCG: Solving for Ux, Initial residual = 0.000742593, Final residual = 7.78633e-07, No Iterations 2 DILUPBiCG: Solving for Uy, Initial residual = 0.000648146, Final residual = 2.82185e-07, No Iterations 2 DILUPBiCG: Solving for Uz, Initial residual = 0.244847, Final residual = 6.20964e-07, No Iterations 2 GAMG: Solving for p, Initial residual = 0.0907169, Final residual = 0.00453577, No Iterations 31 time step continuity errors : sum local = 3.71049e-08, global = 5.32494e-10, cumulative = -4.51107e-09 GAMG: Solving for p, Initial residual = 0.00511943, Final residual = 0.000253917, No Iterations 334 time step continuity errors : sum local = 1.90337e-09, global = 1.51918e-11, cumulative = -4.49588e-09 GAMG: Solving for p, Initial residual = 0.000284638, Final residual = 9.81376e-08, No Iterations 385 time step continuity errors : sum local = 6.5267e-13, global = 7.25236e-15, cumulative = -4.49587e-09 DILUPBiCG: Solving for k, Initial residual = 0.0346825, Final residual = 2.17503e-08, No Iterations 2 bounding k, min: -9.64626e-16 max: 6.49695e-05 average: 7.68376e-09 ExecutionTime = 2903.75 s ClockTime = 2914 s除了decompose的方式不一样之外:
hierarchicalCoeffs // 576 core { n (4 4 36); delta 0.00001; order xyz; }hierarchicalCoeffs // 288 core { n (16 9 2); delta 0.001; order xyz; }其他的设置完全一样。
想问问论坛里有这方面经验的人朋友,愿意分享一下你的经验吗?是从求解器的选择入手?从数值scheme方面,还是decompose的方式? 虽然烧的是国家的机器,但是还是能节省点。LOL。
-
@random_ran
是 GAMG 在拖你的后腿,这么多核的情况下,你可以试试用 PCG + DIC 来求解 p 方程,这个方法并行效率会高一些。 -
谢谢你的建议,确实PCG+DIC 解p方程的效率有所提高,目前新的case还在run。
Time = 0.048 //576 cores Courant Number mean: 0.0211288 max: 0.859123 DILUPBiCG: Solving for Ux, Initial residual = 0.000456629, Final residual = 3.65897e-07, No Iterations 2 DILUPBiCG: Solving for Uy, Initial residual = 0.000477652, Final residual = 4.92182e-07, No Iterations 2 DILUPBiCG: Solving for Uz, Initial residual = 0.235746, Final residual = 6.0203e-08, No Iterations 3 DICPCG: Solving for p, Initial residual = 0.21036, Final residual = 0.0103945, No Iterations 676 time step continuity errors : sum local = 3.27749e-08, global = 2.74055e-11, cumulative = 2.44545e-08 DICPCG: Solving for p, Initial residual = 0.0069283, Final residual = 0.000342288, No Iterations 700 time step continuity errors : sum local = 1.71314e-09, global = -5.01474e-11, cumulative = 2.44043e-08 DICPCG: Solving for p, Initial residual = 0.000423809, Final residual = 2.08942e-05, No Iterations 723 time step continuity errors : sum local = 1.06217e-10, global = 5.3039e-13, cumulative = 2.44049e-08 DILUPBiCG: Solving for k, Initial residual = 0.0159443, Final residual = 3.974e-07, No Iterations 3 bounding k, min: -6.91417e-13 max: 0.0010178 average: 3.66373e-08 ExecutionTime = 1327.45 s ClockTime = 1333 sTime = 0.048 //288 core Courant Number mean: 0.0211368 max: 0.860415 DILUPBiCG: Solving for Ux, Initial residual = 0.000472671, Final residual = 1.86206e-07, No Iterations 2 DILUPBiCG: Solving for Uy, Initial residual = 0.000470667, Final residual = 1.50369e-07, No Iterations 2 DILUPBiCG: Solving for Uz, Initial residual = 0.227442, Final residual = 1.43158e-08, No Iterations 3 GAMG: Solving for p, Initial residual = 0.14952, Final residual = 0.00727048, No Iterations 3 time step continuity errors : sum local = 3.21523e-08, global = 1.32072e-09, cumulative = -2.68714e-11 GAMG: Solving for p, Initial residual = 0.0105374, Final residual = 0.000436311, No Iterations 17 time step continuity errors : sum local = 1.38004e-09, global = 2.02486e-11, cumulative = -6.62288e-12 GAMG: Solving for p, Initial residual = 0.000588406, Final residual = 9.97916e-08, No Iterations 102 time step continuity errors : sum local = 2.47533e-13, global = 3.66548e-17, cumulative = -6.62284e-12 DILUPBiCG: Solving for k, Initial residual = 0.0159342, Final residual = 3.67721e-08, No Iterations 3 bounding k, min: -1.80015e-12 max: 0.00101339 average: 3.66396e-08 ExecutionTime = 1824.48 s ClockTime = 1831 s scalarTransport write: DILUPBiCG: Solving for s, Initial residual = 0.00981188, Final residual = 7.3898e-09, No Iterations 2我把decompose的方式用得和288 cores 那个case 类似
hierarchicalCoeffs //576 case { n (32 9 2); delta 0.001; order xyz; }hierarchicalCoeffs //288 case { n (16 9 2); delta 0.001; order xyz; } -
@cfd-china
你说得很对。从hierarchical到scotch是我要考虑的一个方向。不过由于decompose的时间花费,现在我在处理一些solver上的选择,这样可以不decompse。这个表格是我现在做过的一些case。
我的目标计算时间是1个小时算出0.5second。
#case p-solver #核心数 decompose 方法 数值精度 求解器 1小时后,模拟时间 湍流模型 #PISO 矫正次数 1 GAMG+symGaussSeidel 576 hiera (32 9 2) -6 pisoFoam - LES-kqE 3 2 - - - - - - - - 3 PCG+DIC 576 hiera (32 9 2) -6 pisoFoam 0.133 LES-WALE 3 4 PCG+DIC 576 hiera (32 9 2) -6 pisoFoam 0.129 LES-kqE 3 5 PCG+DIC 576 hiera (32 9 2) -6 pisoFoam 0.125 LES-TKE 3 6 PCG+DIC 576 hiera (32 9 2) -7 pisoFoam 0.125 LES-TKE 3 7 8 9 GAMG+smootherGaussSeidel 576 hiera (4 4 36) -7 pisoFoam 0.015(2914s) LES-TKE 3 10 GAMG+smootherGaussSeidel 288 hiera (16 9 2) -6 pisoFoam 0.171 LES-TKE 2 11 GAMG+smootherGaussSeidel 288 hiera (16 9 2) -6 pisoFoam 0.132 LES-TKE 3 -
$ checkMesh
Create time Create polyMesh for time = 0 Time = 0 Mesh stats points: 34617600 faces: 102296400 internal faces: 100743600 cells: 33840000 faces per cell: 6 boundary patches: 5 point zones: 0 face zones: 0 cell zones: 0 Overall number of cells of each type: hexahedra: 33840000 prisms: 0 wedges: 0 pyramids: 0 tet wedges: 0 tetrahedra: 0 polyhedra: 0 Checking topology... Boundary definition OK. Cell to face addressing OK. Point usage OK. Upper triangular ordering OK. Face vertices OK. Number of regions: 1 (OK). Checking patch topology for multiply connected surfaces... Patch Faces Points Surface topology INLET 28200 28848 ok (non-closed singly connected) OUTLET 28200 28848 ok (non-closed singly connected) CYLINDER 56400 57600 ok (non-closed singly connected) FRONT_CYC 720000 721200 ok (non-closed singly connected) BACK_CYC 720000 721200 ok (non-closed singly connected) Checking geometry... Overall domain bounding box (-20 -20 0) (20 20 3.07458) Mesh has 3 geometric (non-empty/wedge) directions (1 1 1) Mesh has 3 solution (non-empty) directions (1 1 1) Boundary openness (9.81794e-16 9.03981e-18 9.17862e-15) OK. Max cell openness = 3.5214e-16 OK. Max aspect ratio = 229.976 OK. Minimum face area = 7.49334e-07. Maximum face area = 0.022353. Face area magnitudes OK. Min volume = 4.90189e-08. Max volume = 0.00146226. Total volume = 3861.2. Cell volumes OK. Mesh non-orthogonality Max: 4.97612e-05 average: 0 Non-orthogonality check OK. Face pyramids OK. Max skewness = 0.006519 OK. Coupled point location match (average 4.44139e-16) OK. Mesh OK. End -
@random_ran 不知道你运行之前是否 renumberMesh?用了这个之后能减少求解方程时的迭代次数。
另外,还可以尝试 PCG + GAMG,用 GAMG当 PCG 的 smoother。
-
@random_ran 你好,我想问一下,我运用scotch方法剖分了网格,并行运算时提示网格出现下述问题是咋回事:
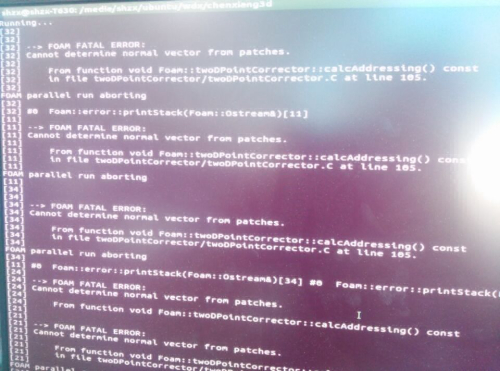
大概提示是找不到法向量,我对应到程序中是这个地方:
103 if (mag(pn) < VSMALL) 104 { 105 FatalErrorInFunction 106 << "Cannot determine normal vector from patches." 107 << abort(FatalError); 108 } 109 else 110 { 111 pn /= mag(pn); 112 } 113大概意思就是分块的面积太小了,找不到法向量?
用simple方法提示的错误不一样,大意几个地方网格的交界面有问题。
可是不管哪个方法,我都检查了网格,checkMesh没问题,单核也可以计算。
我怀疑是不是加密的关系,一般感觉加密的level到3就容易出问题,我这个就到了3,请问你遇到过类似的情况吗?
-
@random_ran 多谢建议,不过确实都没有任何问题。。。
等过一段我贴上来:)
-
好贴子,马住。另外推荐一个连接:
http://nscc-gz.cn/newsdetail.html?6151