k-omega 模型的网格无关性验证

zousiyu

各位老师，大家好！我用标准的 k-omega 模型计算了一个平面自由射流（plane free jet）的案例，分别采用了 4 种不同的网格计算。
网格信息如下，

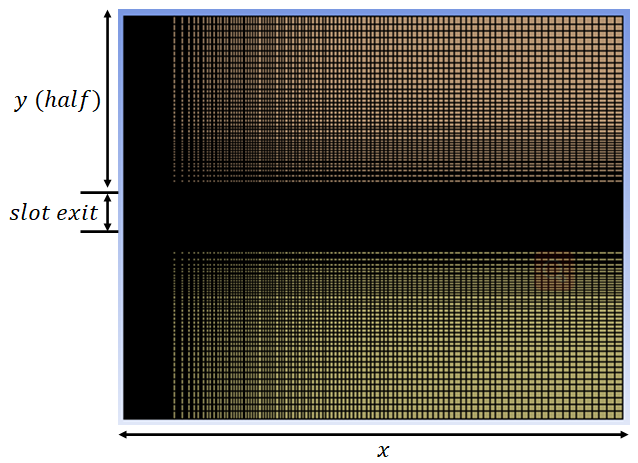
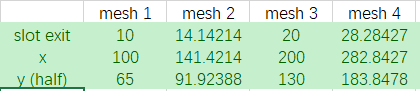
边界条件使用 fluent 常用的设置方式。

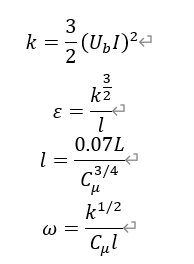
离散格式如图，

计算的残差，mesh 1 和 mesh 2 的 continuity 在 3e-3 左右，其他物理量的残差各异，且无法小于 1e-6。mesh 3 和 mesh 4 的 continuity 在 3e-6 到 6e-6 左右，其他物理量的残差小于 1e-6。
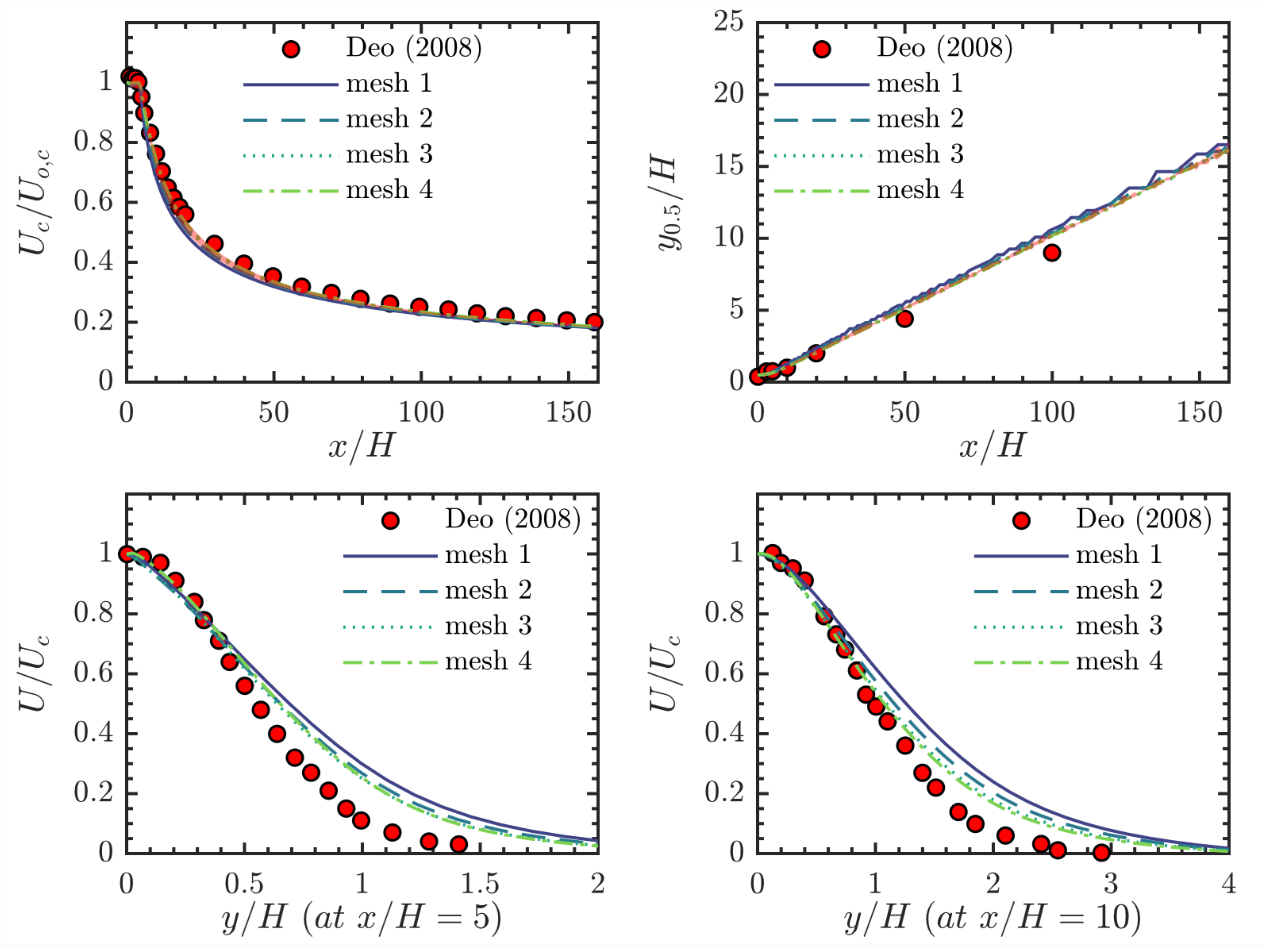
但是这 4 种网格的计算结果并没有显示出网格无关性。结果如图所示，

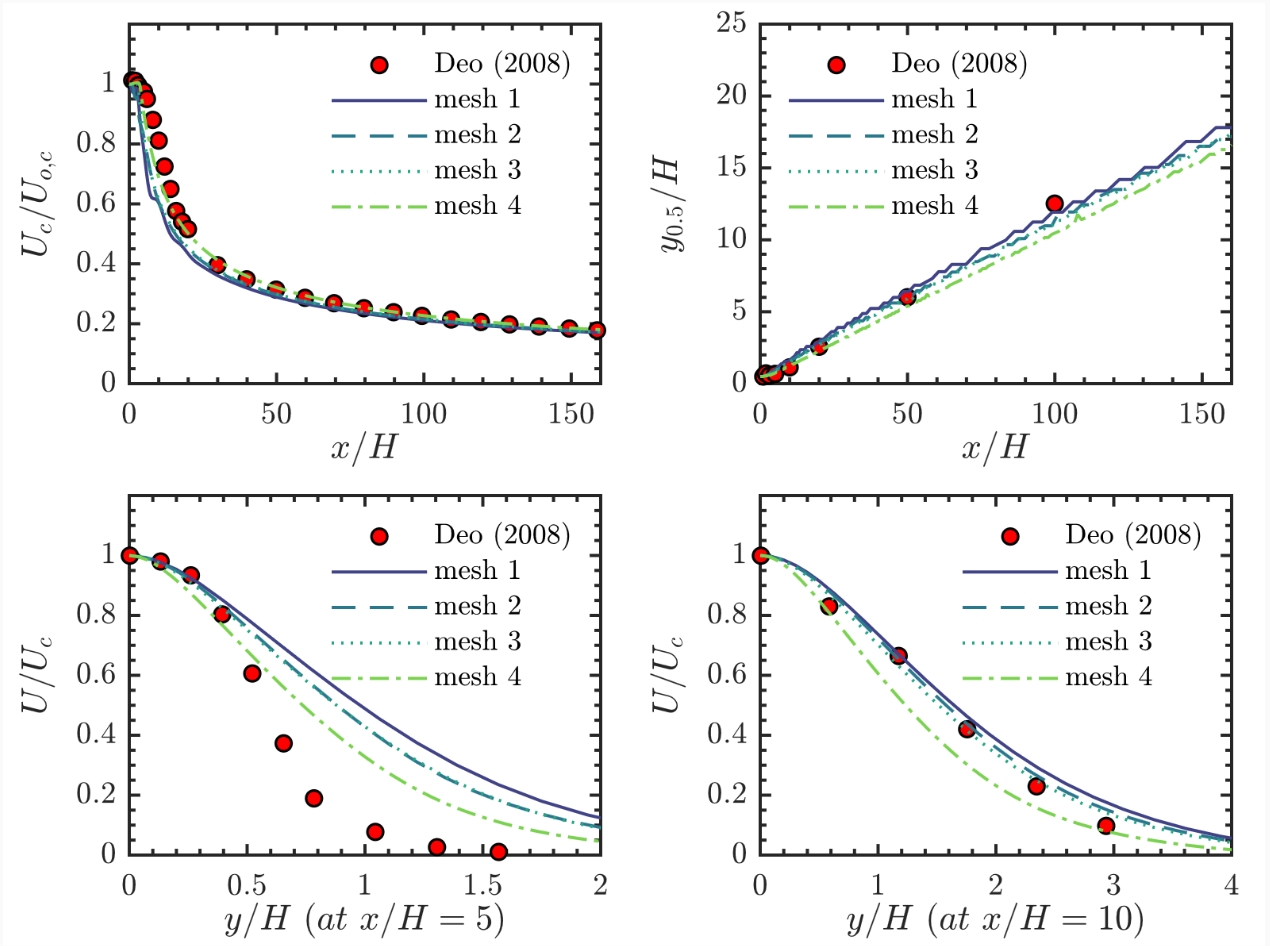
继续加密的 mesh 5 也没有呈现网格无关性。而 k-epsilon 模型非常容易达到网格无关性，mesh 1 到 mesh 4 的结果几乎没有区别。
请教各位熟悉湍流模型的老师，k-omega 模型如何达到网格无关性。

东岳

@zousiyu 你尝试更改过omega的进口条件么

zousiyu

@东岳改成什么呀？

东岳

omega公式中的$l$怎么选取de?

zousiyu

@东岳 $l=0.07L/C_{\mu}^{3/4}$。$L$是射流喷嘴的高度。

zousiyu

@random_ran 老师您可以给一些意见吗？

random_ran

Sorry I had hard time to type Chinese.

Thanks for sharing this. Your finding is consistent with what I've
read this in Wilcox's book (P98).

In free shear flow, k-epsilon model is unaffected by the numerical
value of $k$ and $\epsilon$, but k-omega is very sensitive to the
choice of $\omega$.

But the book does not provide any suggestions on how to achieve mesh
independence on k-omega model.

Speaking to mesh independence study. The idea is simple: refining the
mesh at the region with high gradient. In reality, it depends on
researchers to define where are these regions. Even in the simple
context like flow over a circular cylinder. Different people choose
different types of the computational domain, different strategies to
generate the mesh, different parameters to build the block.

There are something I would investigate:

continue refine the mesh in the "slot exit"
expand the computational domain
expand the "slot exit" region, especially where the shear layers
are.
use unsteady solver
try LES if you have computational resource

Wilcox, D. C., & others, (1998). Turbulence modeling for cfd. : DCW
industries La Canada, CA.

zousiyu

@random_ran 我还有一个想法。书上都说 standard k-omega 模型是一个高雷诺数模型。我图上测试的是 Re=3000 的结果，无法达到网格无关解。我另外测试了一个 Re=16500 的结果，相同的网格，居然可以达到网格无关解。

zousiyu

@random_ran 感谢老师的意见！

Juanyong

图很好看啊，是什么软件做的？

西湖冷月

@Juanyong Origin出这种图应该很容易吧，哈哈

zousiyu

@Juanyong 图是 MATLAB 绘制的，因为可编程才是最灵活的。参见我的文章，https://zhuanlan.zhihu.com/p/85068748

东岳

@zousiyu 图片风格确实不错

zousiyu

@东岳那老师对这个问题有什么看法呢？standard k omega 在 Re=3000 时并不能表现出网格无关性，但相同的条件，在 Re=10000 下可以表现出网格无关性。