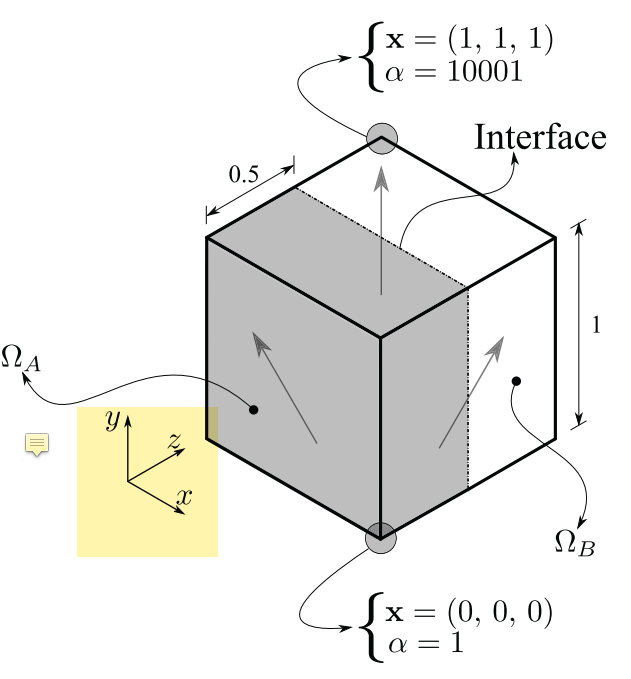
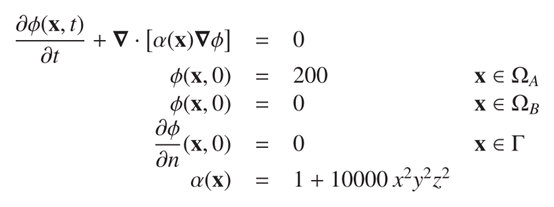关于非均一扩散系数的扩散项离散问题
-
采用二阶精度有限体积法，扩散系数是关于空间位置的函数，面心扩散系数直接给定扩散系数的解析值，扩散项用中心差分格式，时间项用一阶欧拉隐式，计算结果是变量在全域的总积分值会逐渐减少，令扩散系数为常数时计算结果是守恒的。
这种扩散系数应该怎么离散啊。。。
大佬们指点下
-
已经有$\alpha$解析解了还需要离散么？
守恒是什么守恒？全局的$\phi$守恒？
-
单元体积乘单元变量值(在全计算域所有单元求和)，这个积分值和初始场的积分值相等，既是这里指的守恒
-
如果不考虑时间项
\begin{equation}
\int^{f+1}_ {f} \frac{\partial}{\partial x}\left(\alpha \frac{\partial \phi}{\partial x}\right)\mathrm{d}x=\left(\alpha \frac{\partial \phi}{\partial x}\right)_ {f+1}-\left(\alpha \frac{\partial \phi}{\partial x}\right)_ {f}
\end{equation}
把后面两项$\left(\alpha \frac{\partial \phi}{\partial x}\right)_ {f+1}-\left(\alpha \frac{\partial \phi}{\partial x}\right)_{f}$把所有的面连起来，看起来是守恒的，剩下的只有边界条件
