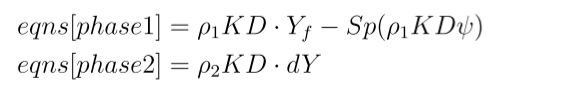reactingTwoPhaseEulerFoam求解器的组分输运方程中添加质量源相导致质量分数无界

[zwl]

reactingTwoPhaseEulerFoam求解器的组分输运方程中添加质量源相导致质量分数无界，这是什么原因，为什么没添加源相之前有界呢？如何处理才能避免质量分数远大于1？

[东岳]

是的，添加源项会导致越界。$\frac{\p \phi}{\p t}+\bfU\cdot\nabla\phi=S$，只有在$S=0$的时候才有界。目前只能帮你到这里了

[zwl]

@东岳 非常感谢东岳老师的回答，我有个疑问，这个求解器是可以算蒸发的，而且用的就是界面组分，他们是怎么处理的呢？就避免了越界。

[东岳]

@zwl 你是说植入的Y方程么

[zwl]

@东岳 对，就是自带的Y方程。

[东岳]

Y方程没有详细看过。粗略看一眼并没有用MULES求解。另外，带源项要有界可以参考可压缩的相方程

[yfclark]

@zwl 会不会是源项处理有问题，求解不稳定，Interface Composition搞了个fvm::Sp:

此外可以考虑更换对流项格式，Laneer，Gamma01等

[zwl]

@yfclark 非常感谢你的建议。源相我确实是直接添加的，没有再做处理，这个Sp会有什么作用（虽然有时我也会模仿着这样处理）？越界的主要原因是什么？

[zwl]

@东岳 那么下面带拉普拉斯项的组分输运方程如何采用MULES求解呢？谢谢。

        fvm::ddt(alpha, rho, Yi)
      + fvm::div(alphaRhoPhi, Yi, "div(" + alphaRhoPhi.name() + ",Yi)")

      - fvm::laplacian
        (
            fvc::interpolate(alpha)
           *fvc::interpolate(this->muEff()/Sct_),
            Yi
        )
     ==
        alpha*this->R(Yi)
       + Source
      + fvc::ddt(residualAlpha_*rho, Yi)
      - fvm::ddt(residualAlpha_*rho, Yi)

[东岳]

扩散项+对流项用高阶/低阶格式处理，通过反扩散算法做出通量，源项进Sp或者Su就行

[zwl]

@东岳 我看MULES代码，感觉他就是为求解相方程定制的，没有扩散相的处理，所以我不知道这里的扩散相放在哪个位置，怎么处理。

[东岳]

@zwl 扩散项、梯度项、对流项都是通过高斯定律化为$\sum$加和的形式，都是一样的，以梯度项举例：

[东岳]

对了，扩散项不会引起越界问题，或许你都不用处理了，扩散项是好朋友

[东岳]

@zwl 你在研究E-E模型下面的组分传输么

[zwl]

是的，求解器自带的是蒸发，我想计算空化，二者的计算原理大不相同，我更改了质量源相，导致质量分数越界。