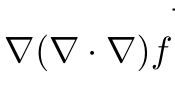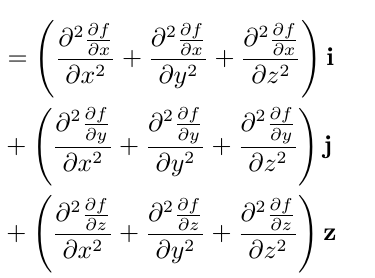关于一个表达式的笛卡尔分解问题
-
遇到一个表达式
不知道分解成为笛卡尔应该怎么分解
我个人意见是
不知道对不对？
-
$$
\begin{aligned}
\nabla(\nabla \cdot \nabla) f
&=
\nabla \left(\frac{\partial^{2} f}{\partial {x}^{2}}+\frac{\partial^{2} f}{\partial {y}^{2}}+\frac{\partial^{2} f}{\partial {z}^{2}}\right)\
&=\frac{\partial}{\partial x}\left(\frac{\partial^{2} f}{\partial {x}^{2}}+\frac{\partial^{2} f}{\partial {y}^{2}}+\frac{\partial^{2} f}{\partial {z}^{2}}\right) \vec i+\frac{\partial}{\partial y}\left(\frac{\partial^{2} f}{\partial {x}^{2}}+\frac{\partial^{2} f}{\partial {y}^{2}}+\frac{\partial^{2} f}{\partial {z}^{2}}\right) \vec j+\frac{\partial}{\partial z}\left(\frac{\partial^{2} f}{\partial {x}^{2}}+\frac{\partial^{2} f}{\partial {y}^{2}}+\frac{\partial^{2} f}{\partial {z}^{2}}\right) \vec k
\end{aligned}
$$
-
@wwzhao 您好 感谢您的回答 对我帮助非常大 再次想请教下 是否可以换序成为我的那种形式 因为这种形式在程序编写方面 有一定的障碍 在fluent UDF
-
@l-j刘侃 求导符号可以交换，所以把偏导放到括号里面的 $f$ 前面也是可以的。
-
@wwzhao 再次感谢
