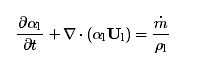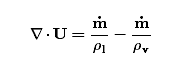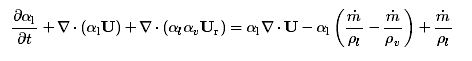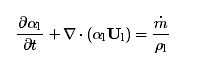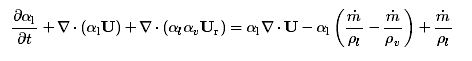关于interPhaseChangeFoam和boundedness的疑问

[Jacobian]

第一相的体积分数输运方程为：

但实际求解的时候要利用：

将方程改写为：

我的疑问是，为什么要将alpha1*divU引入原方程中呢？它的作用如何用数学语言表达？

[李东岳]

方程右边的alpha1*divU是对方程左边操作的附加产物，方程

中的对流项不能保证有界因此变成了

[Jacobian]

@李东岳 谢谢东岳老师的回复！
但是为什么说原方程的对流项不能保证有界呢？

[李东岳]

因为$\nabla\cdot\mathbf{U}_1 \neq 0$

[Jacobian]

按照我浅薄的理解，有界往往是通过差分格式（如TVD格式），或者对流项特殊处理方法（如FCT）来完成的。所以没有想通 alpha1*divU 究竟对保证有界究竟有何贡献？如何用数学语言分析它的作用？
另外，问题的来源是这样的：我结合compressibleInterFoam和interPhaseChangeFoam改编了一个包括水、水蒸气、不可凝结气体的三相带空化的可压缩求解器。目前有一个困扰了我很长时间的bug，如果存在不可凝结气体设置为fixedValue uniform 1的边界（如带有自由面问题的最上方的大气），水中本应该发生空化的地方莫名其妙产生不可凝结气体。很肯定空化模型没有写错，所以认为问题很可能出现在alphaEqn的源项处理上不得当，不得不深挖一下其中的细节。
如果前辈对引入divU 的作用解释得再详细一点就好了！求甩我一脸文献！ @李东岳
欢迎研究类似问题的朋友们一起来讨论！

[李东岳]

http://www.cfd-china.com/assets/uploads/files/1516800015640-wcm0001.pdf

[yhdthu]

@李东岳 前辈好分析，我还有个问题，为啥在用MULES隐式修正的时候，div(U)又归于Su了呢？ 这个MULES::correct如何用的呢？

      MULES::correct
        (
            geometricOneField(),
            alpha1,
            talphaPhi(),
            talphaPhiCorr.ref(),
            vDotvmcAlphal,
            (
                divU*(alpha10 - alpha100)
              - vDotvmcAlphal*alpha10
            )(),
            1,
            0
        );

[李东岳]

@yhdthu 目前还没分析到MULES隐式那面

[yhdthu]

@李东岳 前辈，我还有个问题，在通量修正时，为啥第二个压缩项要写成两个负的？如果不这样有啥区别么？:surprised:

fvc::flux
            (
                phiV,
                alpha1,
                alphaScheme
            )
          + fvc::flux
            (
                -fvc::flux(-phir, alpha2, alpharScheme),
                alpha1,
                alpharScheme
            )

[mohui]

@李东岳 看完之后，还是有点没明白，对于偏微分方程来说，等式右边不为0为什么就说是无界？望解答，谢谢。

[yuan_neu]

@yhdthu 相方程里面的divU是描述可压缩性的影响的
而且方程式求解alpha，自然是做显性处理

[李东岳]

-fvc::flux(-phir中的flux要调用离散格式，这样做是为了适用下风格式。比如fvc::flux(-phir...和fvc::flux(phir...在进行插值的时候是不同的。

[litong189456]

@东岳
东岳前辈，我看您的一篇文章《Simulation of bubbly flows with special numerical treatments of the semi-conservative and fully conservative two-fluid model》，其中关于可压缩相方程boundness这里有一点没看懂，可以请您详细解释一下吗？

[李东岳]

@mohui 若有方程
\begin{equation}
\frac{\p \alpha}{\p t}=S\neq 0
\end{equation}
很明显$\alpha$是无界的。

[李东岳]

考虑方程30的一维形式

\begin{equation}
\frac{\p \alpha}{\p t}+\frac{\p \alpha u}{\p x}+\frac{\p \alpha\beta u_r}{\p x}=\alpha\beta\mathrm{dgdt}+\alpha\frac{\p u}{\p x}
\end{equation}
由于
\begin{equation}
\frac{\p u}{\p x}\neq 0
\end{equation}
有
\begin{equation}
\frac{\p \alpha}{\p t}+\alpha\frac{\p u}{\p x}+u\frac{\p \alpha}{\p t}+\frac{\p \alpha\beta u_r}{\p x}=\alpha\beta\mathrm{dgdt}+\alpha\frac{\p u}{\p x}
\end{equation}
\begin{equation}
\frac{\p \alpha}{\p t}+u\frac{\p \alpha}{\p t}+\frac{\p \alpha\beta u_r}{\p x}=\alpha\beta\mathrm{dgdt}
\label{bound}
\end{equation}
方程\eqref{bound}为波方程的形式，第一项和第二项必然有界。第三项和第四项，在$\alpha$等于1或者0（界限）的时候，也为0，方程进一步的在界限处不会越界。

[李东岳]

如果有用，很高兴你们能引用这篇文章 Simulation of bubbly flows with special numerical treatments of the semi-conservative and fully conservative two-fluid model