Smagorinsky模型系数问题
-
- 李老师,看评论区并根据Sullivan论文,第一种方法应修改为:$\nu _t =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $。评论区大佬说的是of中默认值
Ck=0.094, Ce=1.048,可以计算得到默认值Cs=0.167,这个数值是根据各向同性湍流的得到的。
-
我对湍流模型不太懂,但想到一个猜测观点:
(1) 如果用第一种方法指定$C_s$,根据$C_s=\left ( C_k \sqrt{\frac{C_k}{C_e} } \right ) ^{1/2}$,理论上反推的$C_k$和$C_e$就无法唯一确定,也就是说,一个$C_s$值是可以对应很多对$C_k$和$C_e$,比如采用Cs=0.065,那么可以取Ck=0.026546355, Ce=1.048或者Ck=0.04, Ce=3.585308638等很多组合。但可能第一种方法推导采用了ksgs的生成与耗散平衡假设,因此实际反算的$C_k$和$C_e$是与这种假设唯一相对应的。
(2) 如果用第二种方法,通过指定Ck=0.026546355, Ce=1.048,就可以唯一确定Cs=0.065。也就是说,可以动态指定$C_k$和$C_e$的取值对计算结果的作用程度,并且自然满足所预期的$C_s$。 -
结合下面这位大佬的评论,猜测第一种方法就默认ksgs的生成与耗散平衡,而第二种方法可以动态指定$C_k$和$C_e$,来反映ksgs的生成与耗散的非平衡关系?也就是第二种方法比第一种方法适用范围更广,当$C_k$和$C_e$能够取平衡状态的值,那么两种方法就是等价的?
- 李老师,看评论区并根据Sullivan论文,第一种方法应修改为:$\nu _t =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $。评论区大佬说的是of中默认值
-
1. 采用第二种方法:
(1)根据Smagorinsky SGS model in OpenFOAM | CFD WITH A MISSION的推导,基于式(5)的
Local equilibrium假设,对于incompressible flows,才能得到式(8)关系,进而得到式(10)和(11)。然后将式(11)与文献中的公式(12)对比,得到式(13)关于$C_e, C_k, C_s$三个系数的关系式。



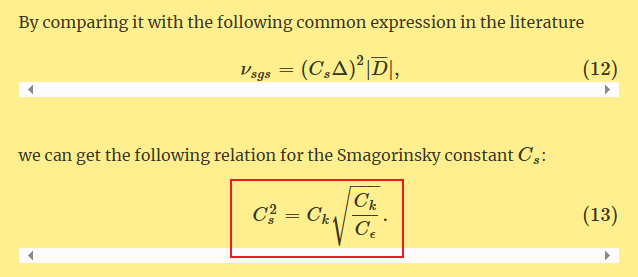
(2)现在分析式(10)和(11)。
-
首先这两个公式是基于
Local equilibrium假设得到的,将式(10)和(11)代入式(5),得到的结果自然满足Local equilibrium假设。 -
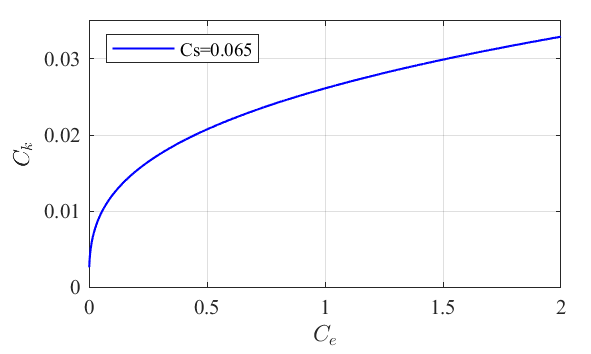
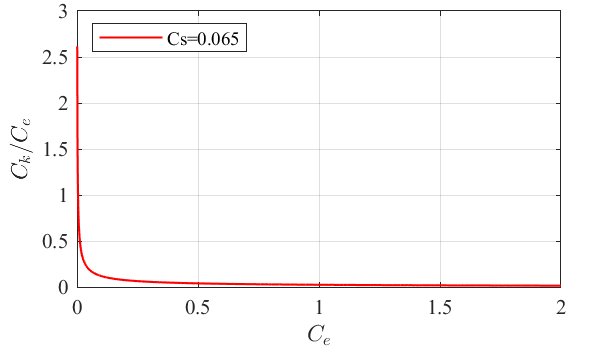
接着看式(11),我们可以通过设置合适的$C_e$和$C_k$,来实现等价的$C_s$。但是,式(10)中$k_{sgs}$的值与$C_k/C_e$这个比值相关联的。换句话说,计算设置满足了等价的$C_s=0.065$,但$C_k, C_e$可以有多种不同组合,这将导致$k_{sgs}$计算结果可能差别很大。根据式(13),可以得到:$C_k = \left ( C_eC_s^4 \right ) ^{1/3}$,以固定取$C_s=0.065$为例,画图如下。可以看出$C_e$取值越小,$C_k/C_e$比值变化越剧烈。表明了虽然结果都是满足
Local equilibrium假设以及实现了$C_s=0.065$,$C_e$和$C_k$仍然要取合适的组合,才能得到合理的$k_{sgs}$
2. 采用第一种方法:
个人疑问是植入:$ \nu _{sgs} =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $ ,
那么式 (1d) 中的$k_{sgs}$是怎么计算的?这会不会就是两个方法的主要差别?
-
-
我最近看到一个老版本的动态模型植入。植入的不是$\nu_{sgs} =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $,而是$\nu_{sgs} =\left ( C_s \Delta\right )^2 \sqrt{ \mathbf{D} :\mathbf{D} } $,大佬怎么看
-
@李东岳 李老师, 这两个链接在讨论
of中的Smagorinsky模型时,也类似讨论of中为何植入的是$\sqrt{ \mathbf{D} :\mathbf{D} } $,相比理论公式看似缺少$\sqrt{ 2} $系数。但其实是一致的,这是因为of中把$\sqrt{ 2} $加到了前面的系数中。下面截图中的理论公式符号代表:$\left | \bar{S} \right | = \sqrt{2 \mathbf{D} :\mathbf{D} } $,但OF公式代表:$\left | \bar{S}_{of} \right | = \sqrt{ \mathbf{D} :\mathbf{D} } $,在CFD-online上的帖子因为把符号写成一样导致了混淆。
Smagorinsky model details -- CFD Online Discussion Forums
[转载]有关OpenFoam中LES smagorinsky模型的推导_馨予_新浪博客
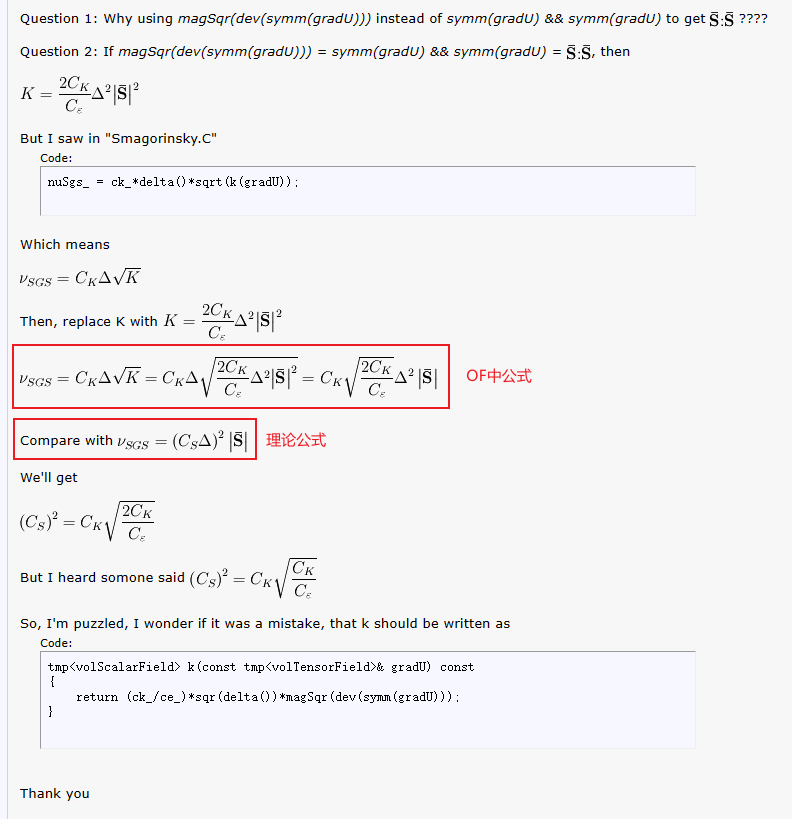
湍流模型我不太懂,在想
dynSmagorinsky是否类似于CFD-online的讨论,是否也是把系数$\sqrt{ 2} $加到了前面的系数中?也就是cD(D)可能比dynSmagorinsky理论公式多了$\sqrt{ 2} $系数?void dynSmagorinsky::updateSubGridScaleFields(const volSymmTensorField& D) { nuSgs_ = cD(D)*sqr(delta())*sqrt(magSqr(D)); nuSgs_.correctBoundaryConditions(); } -
@李东岳 这个公式结论是对的,不用加$\sqrt{2}$。CFD-online讨论帖子初始问题混淆点是把OF计算的$\sqrt{ \mathbf{D} :\mathbf{D} } $当做$\left | \bar{S} \right | $,而理论公式的$\left | \bar{S} \right | $表示的是$\sqrt{2 \mathbf{D} :\mathbf{D} } $。OF是单独计算了$\sqrt{ \mathbf{D} :\mathbf{D} } $,为与理论对应,$\sqrt{2}$在前面的系数里计算再相乘。
Smagorinsky SGS model in OpenFOAM | CFD WITH A MISSION这个帖子推导就没有混淆符号,统一用$\sqrt{2 \mathbf{D} :\mathbf{D} } $表示$\left | \bar{S} \right | $

-
 李 李东岳 被引用 于这个主题
李 李东岳 被引用 于这个主题
-
对,因为湍流模型不太懂,我猜测
dynSmagorinsky差个$\sqrt 2$可能是这个原因。Smagorinsky模型不是直接植入这个公式,是通过把系数代入$\nu_{sgs}=C_k\Delta \sqrt{k_{sgs}}$后得到等价的$\nu_{sgs}=C_k \sqrt{\frac{2C_k}{C_e} } \Delta ^2 \sqrt{\mathbf{D} :\mathbf{D} }
=C_k \sqrt{\frac{C_k}{C_e} } \Delta ^2 \sqrt{2\mathbf{D} :\mathbf{D} }=\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $ -
@李东岳 在 Smagorinsky模型系数问题 中说:
你的意思就是,OpenFOAM里面植入的应该是$\nu_{sgs} = (C_s^{of})^2 \Delta^2 \sqrt{ \mathbf{D} :\mathbf{D} } $,其中$(C_s^{of})^2=C_s^2\sqrt{2}$
而不是$\nu_{sgs} = C_s^2 \Delta^2 \sqrt{ \mathbf{D} :\mathbf{D} } $
是这样么
https://bugs.openfoam.org/view.php?id=816
这个确实是个bug,不过OpenFOAM新版已经把动态Smagorinsky删掉了,所以无关紧要了。
-
我按照$\nu_t=(C_s\Delta)^2\sqrt{2\bfS:\bfS}$的方式植入进入了。从云图来看没啥区别。希望有大佬来详细验证一下是否均衡。下面这个文件,可以在OpenFOAM-10下进行编译,步骤:
wmake cd pitzDaily ./Allrun注意算例中的$C_k$的值忘记改了,应该改为0.065
个人疑问是植入:$ \nu _{sgs} =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} }$ 那么式 (1d) 中的k是怎么计算的?这会不会就是两个方法的主要差别?
@coolhhh 应该是从$\nu_t$反推出来的,$k=\nu_t^2/(C_k\Delta)^2$