粘弹性流体高Wi数时间步长步进问题

沐风

最近在采用openFoam下的开源工具rheoTool模拟高Wi数下粘弹性流体upstream flow问题，主要对照这篇论文进行算法植入：https://arxiv.org/ftp/arxiv/papers/2203/2203.09239.pdf
但是运行瞬态case发现在小时间步长0.0001s下算例能稳定运行，但是发现算例无时间步进特征，一直保持稳态特征。将时间步长增加至0.001s时发现算例会短暂呈现论文中的upstream flow特征，但流动发展一会算例就会崩掉。
按理说小时间步长在保持运行稳定同时应该有步进特征才对，同时按照东岳大佬最近的推文，方程的松弛因子我都设置的1.0
solver和case均上传了，麻烦各位路过大佬看下给点建议，有偿也可以，谢谢！solver-case.zip

李东岳

我记得rheoTool本身就已经植入了黏痰流体的算法。你是进一步的做了改动么？

沐风

@李东岳链接的论文中在变形张量方程中考虑了分子扩散也就是变形张量方程中增加了拉普拉斯项，因此我在rheoTool基础上增加了这一项，用的F-P模型，变形张量输运方程中的sqrt重构。搞不懂小时间步长下为什么不步进发生流动，费解ing

沐风

@李东岳在粘弹性流体高Wi数时间步长步进问题中说：

我记得rheoTool本身就已经植入了黏痰流体的算法。你是进一步的做了改动么？

我求解过程也是按照论文描述来的，搞不懂问题出在了哪里

李东岳

改动不多的话可以把你的代码贴一下，类似这种：

源代码

以下是我的代码
ssss
以上是我的代码

源代码

沐风

@李东岳目前主要参考了rheoTool中已有的O-B模型sqrt重构代码进行F-P模型sqrt重构。已有O-B模型sqrt重构的变形张量输运方程为(https://www.sciencedirect.com/science/article/pii/S0377025711000504?via%3Dihub)：

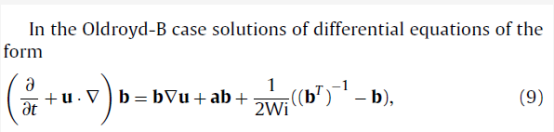
对应rheoTool中已经有代码为：
// Stress transport equation
fvSymmTensorMatrix bEqn
(
fvm::ddt(b_)
+ fvm::div(phi(), b_)
==
symm((b_&L) + (a & b_))
+ (0.5/lambda) * inv( b_.T() )
- fvm::Sp(0.5/lambda, b_)
);
bEqn.relax();
bEqn.solve();
考虑分子扩散项的F-P模型变形张量sqrt重构输运方程为：（https://www.sciencedirect.com/science/article/pii/S0377025711000504?via%3Dihub）（https://arxiv.org/ftp/arxiv/papers/2203/2203.09239.pdf）

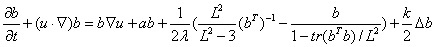
对于F-P模型，为了保证tr(ckk)=tr(bTb) 有界，也就是tr(bTb)<L2，论文作者在每个时间步进前进行了如下处理：

图中2-9即为tr标量输运方程，但是对比2-7，作者2-9右边第一项忘写了tr符号，正确的tr输运方程应该为：

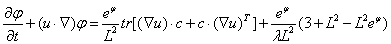
因此在rheotool的rheoFoam求解器下每个时间步进前植入了如下方程：
{
// Velocity gradient tensor
volTensorField L1 = fvc::grad(U);

volTensorField j = (b.T() & b) & L1;

fvScalarMatrix dEqn
(
    fvm::ddt(d) 
  + fvm::div(phi, d)
  ==
  (tr(twoSymm(j)) / L2) * Foam::exp(d)
 + ((3 + L2) / (lambda * L2)) * Foam::exp(d)
 - (1 / lambda) * Foam::exp(d) * Foam::exp(d)   
);
dEqn.relax();
dEqn.solve();

}
同时对于:

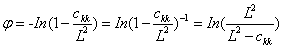
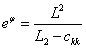
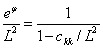
因此基于F-P模型的sqrt重构对称张量b输运方程为：

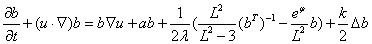
对应植入代码为：
fvSymmTensorMatrix bEqn
(
fvm::ddt(b)
+ fvm::div(phi, b)
==
symm((b&L) + (a & b))
+ (0.5/lambda) * inv( b.T() ) * (L2 /(L2-3))
- fvm::Sp((0.5/lambda) * (exp(d) / L2), b)
// - fvm::Sp(0.5/(lambda * (1-(tr(b.T() & b) / L2))), b)
+ fvm::laplacian(0.5 * k, b)
);

bEqn.relax();
bEqn.solve();

沐风

@李东岳烦请东岳老师有空看下，期待您的回复。谢谢！