DNS出口边界条件
-
前一段时间一直在算空气在加热圆管流动的DNS，目前算了两秒多，还在算，残差保持稳定，但数量级有点高，p跟U稍低于0.01.平均壁温还没有达到光滑分布。我对于速度出口设成 advictive 不太有把握，这个边界的原定目的是想消除反射波。另外对于DNS收敛的监测角度，有什么比较有效的判据吗？谢谢。
最近还在国家超算上用DNS算超临界CO2的圆管对流换热，热物性变化十分剧烈。后面看看情况。
-
残差保持稳定，但数量级有点高，p跟U稍低于0.01.平均壁温还没有达到光滑分布。我对于速度出口设成 advictive 不太有把握，这个边界的原定目的是想消除反射波。
什么反射波？
-
@东岳 这边放上相关的描述
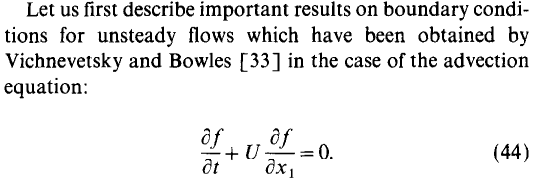
您觉得对于加热圆管流动的DNS来说，需要这种边界条件吗？OpenFOAM自带的有advective BC。
-
这个图是求解双曲波方程的，你求解的方程有44这种形式的么？
-
@东岳 谢谢。
这是一篇也做超临界二氧化碳DNS的论文的部分截图
里面是建议用convective boundary condition。在OpenFOAM里面有自带的advective BC，植入的方程应该就是这个。
我用湍流模型算的时候，如果用advective BC，残差会出现大幅震荡的情况，如果用inletoutlet就不会出现；在DNS里面用advective，现在残差倒是很平稳，但不知道有没有起到效果。 -
如果方程30是速度3个速度分量的传输方程的话，看起来没有粘度和压力项？
-
@东岳 不清楚诶
这些是控制方程
-
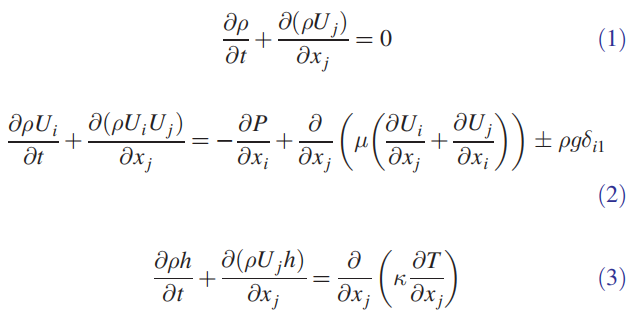
@东岳 两篇：
Direct Numerical Simulation of Heated Turbulent Pipe Flow at Supercritical Pressure ---Xu Chu，Eckart LaurienDirect numerical simulation of turbulent supercritical flows with heat transfer ---Joong Hun Bae, Jung Yul Yoo, and Haecheon Choi
-
我看了第一篇文章，
The outlet boundary condition for the velocity is the convective boundary condition from
Orlanski [19], as seen in Eq. (5), where ϕ could be any scalarvariable or the velocity vector and Uc is the convective velocity
of the outflow
Orlanski [19] 的方法是用于描述双曲方程的，我不觉得你之前的贴图有任何一个是双曲方程。你为什么要用advective边界条件？为什么不用zeroGradient？
-
@东岳 我看的DNS文章里面，都是用这个convective boundary作为速度出口，我的控制方程跟他们的一样。所以我就借鉴了。
另外我对比了advective跟inletoutlet两种边界对结果有何影响，对比如图示：
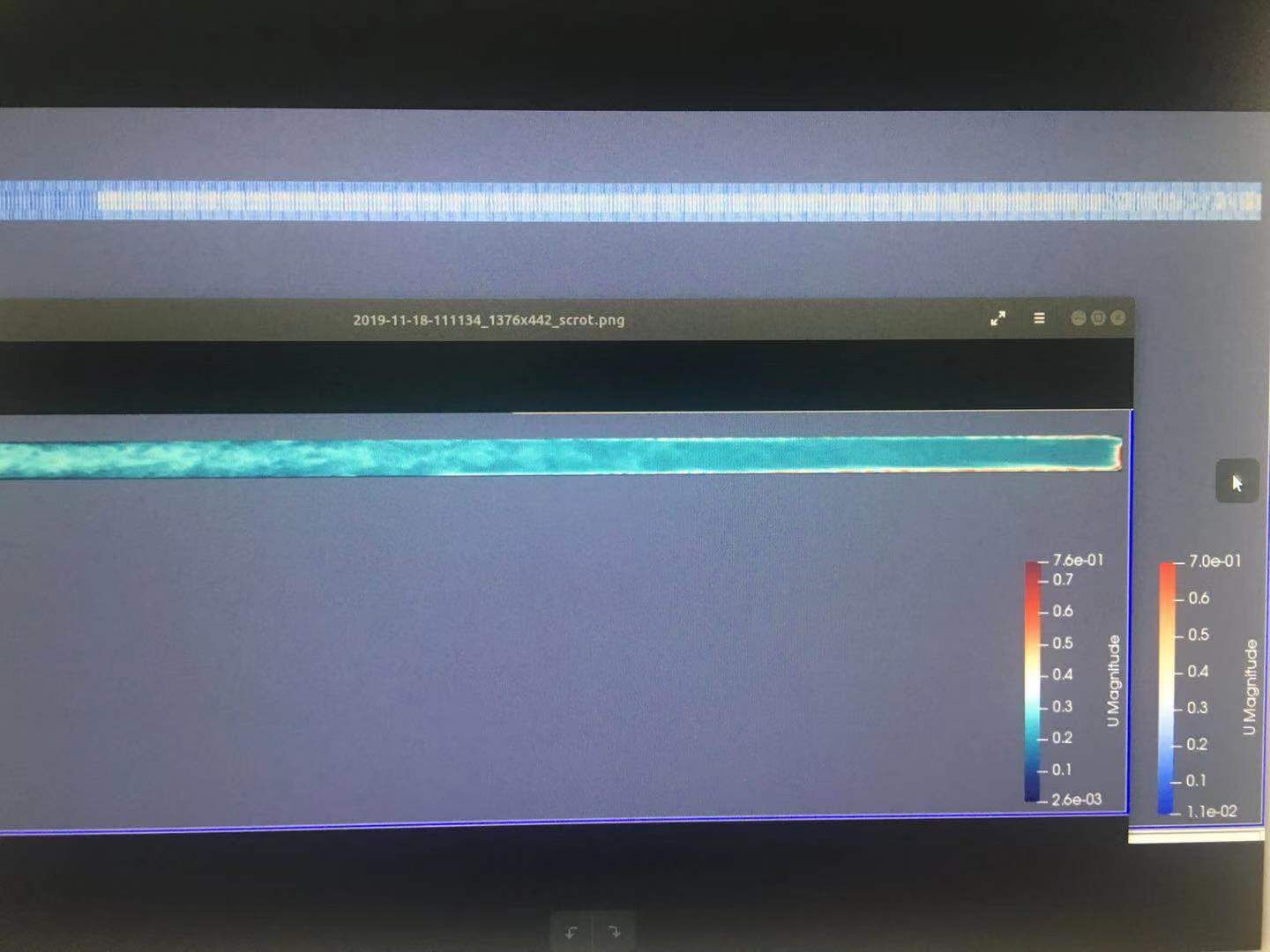
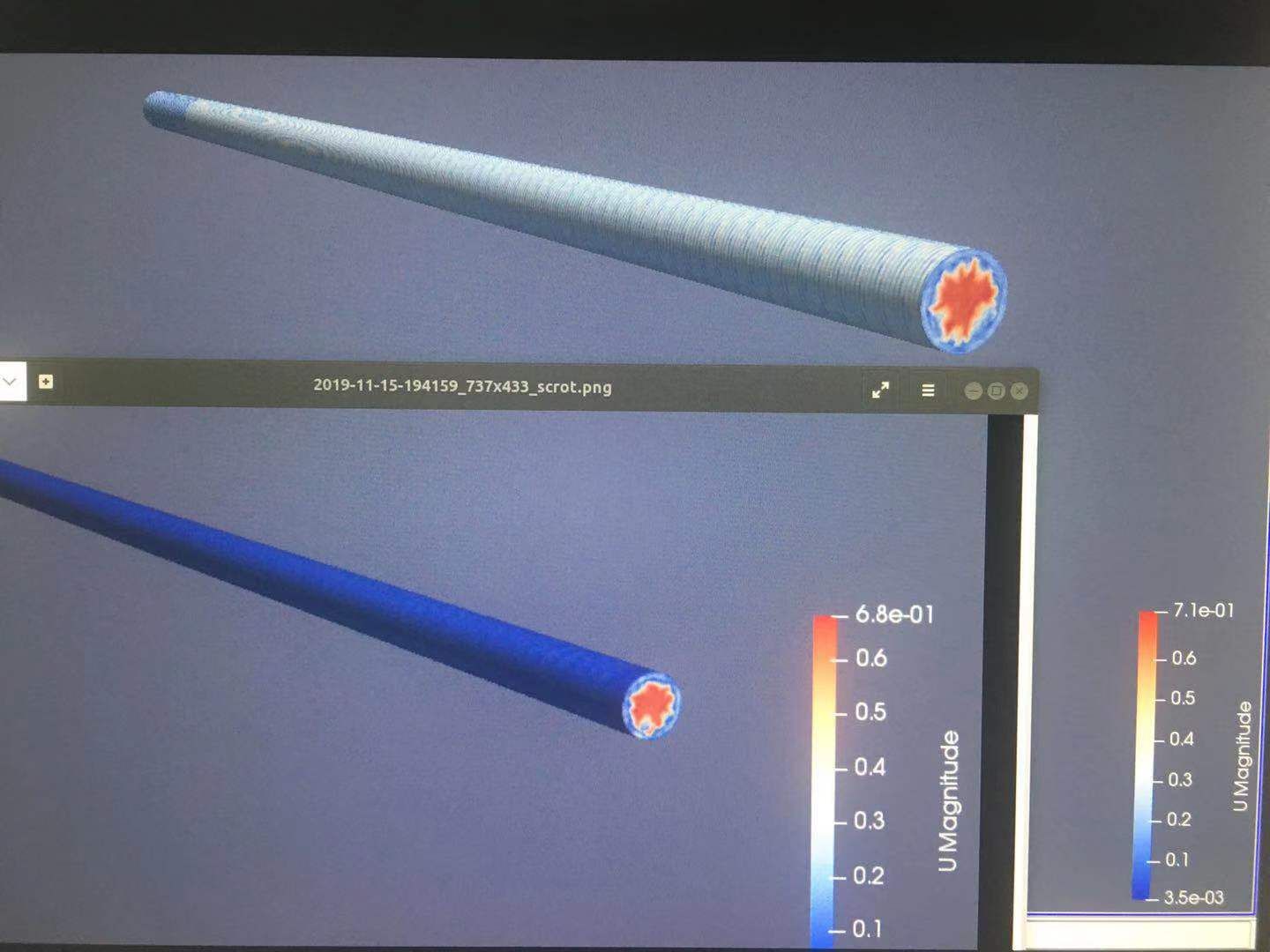
两张图的上面部分是inletlet，出现了很奇怪的现象。下面部分是advective，不太理解的是第一张图的下半部分，右端出口处有速度的突增，不知道怎么解释这种情况？谢谢。 -
很明显N-S方程里面，并不存在标量传输，速度分量传输方程也不符合方程30。我没看到N-S系统里面有方程30的存在。在进一步讨论之前，我要看看文献里怎么讨论的这个方程。现在sci-hub挂掉了，上班时候我回复你
-
@东岳 好的谢谢！
-
Orlanski反射边界条件用于消除双曲系统的反射波，在Orlanski原始文章中也提及他提出的无反射边界条件适用于双曲系统，但Orlanski自己也说：
A Sommerfeld radiation condition (2.2) is proposed for problems requiring a prescribed open boundary. The equations must be hyperbolic in nature (although the author believes that they may also be good for some elliptic and parabolic problems)
但是很明显DNS方程不是双曲系统，但是很多DNS模拟的文章我确实看到了都在用无反射边界条件。这我有点搞不懂了。我找了一些sci，没有一个有一个合理的解释。大部分就是表明：本文用的这个无反射边界条件，然后把Orlanski的文章引上，没解释为什么。即使一些有解释，也说用于双曲系统，blahblahblah，但是很明显DNS不是双曲系统
只到我发现一篇。我看起来解释是合理的
翻译过来（我的理解）就是：对于一般的比如RANS这种抹平湍流结构很严重的模型，扩散项主宰，方程类型偏向抛物，可以用零发现梯度。但是对于DNS这种，湍流结构很严重，对流很严重，偏向双曲，因此可以使用无反射边界条件
至少这个解释是合理的
In case of diffusion-dominant flows or flow scenarios where advection gets balanced by diffusion; a homogeneous Neumann condition in momentum serves as a reasonably accurate description of flow exiting the domain. However, applicability of this condition deteriorates with increasing Re as the regime progressively becomes advection-dominant and probability of the flow (nonphysically) reflecting inward from the boundary increases. Naturally, a need arises to establish nonreflecting exit boundary conditions for advection-dominant flows.
https://www.tandfonline.com/doi/pdf/10.1080/10407790.2019.1580952?needAccess=true
https://www.tandfonline.com/doi/pdf/10.1080/19942060.2016.1247296
对于你的文章，如果你感兴趣，你可以专门对比一下这两个边界条件对你结果的影响，主要要看plot不能看云图，然后分析下结果，估计也就是半页纸。证明边界条件对你的结果没有影响。然后附加类似上面这一段话的描述。证明为什么你对NS方程（而不是双曲欧拉方程）施加了一个无反射边界条件
另外，如果你能加上这句话更好：
@Calf-Z-DNS would like to acknowledge the small, but active, CFD community in China (CFD-China) for the fruitful discussions of numerical settings employed in this work.
当然这都是文献上的讨论，具体你用零发现梯度还是无反射，只能对比看你的算例哪个更使用
-
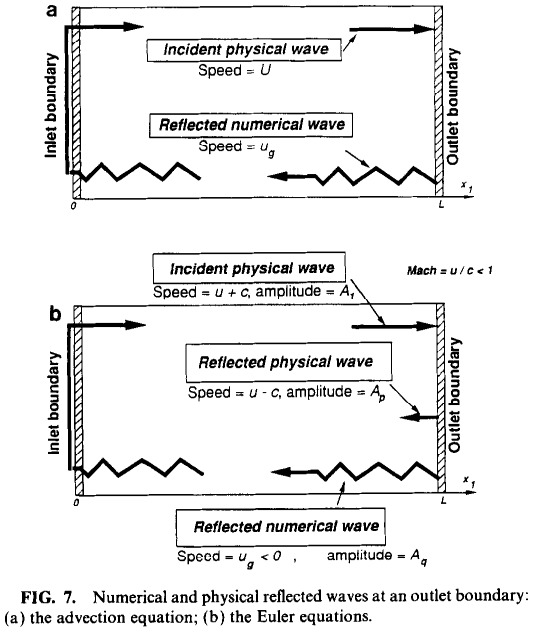
@东岳 非常感谢耐心的解答和分析！颇有启发！
我有大致对比过advective跟inletoutlet的效果，如上面的图所示，不理解的是advective在出口处为何有个速度突增。但另一个边界条件的结果显得更为离谱，我简单plot了其壁面的速度分布，是疯狂地震荡。根据您以上的分析，advective似乎更合理。我如果有发表类似论文，乐意提及CFD-China对论文工作所做的贡献。 -
我更新一个advective边界条件的解释，你看看。类似内容没看到有任何英文资料解释的这么详细，none of them is satisfactory。因此要是中文的。理论解释最好有数值验证，不过目前我没空做，谁感兴趣可以验证一下
https://www.jianguoyun.com/p/DdvrhJMQ9s3ZBhjw7p4B
-
@Calf-Z-DNS 你好有关于对流传热的问题想要咨询下你，就是对流出口边界条件的设置问题，是只对U使用的，还是全部都用呢？
-
@Calf-Z-DNS 好久没联系 你的DNS算的怎么样了
