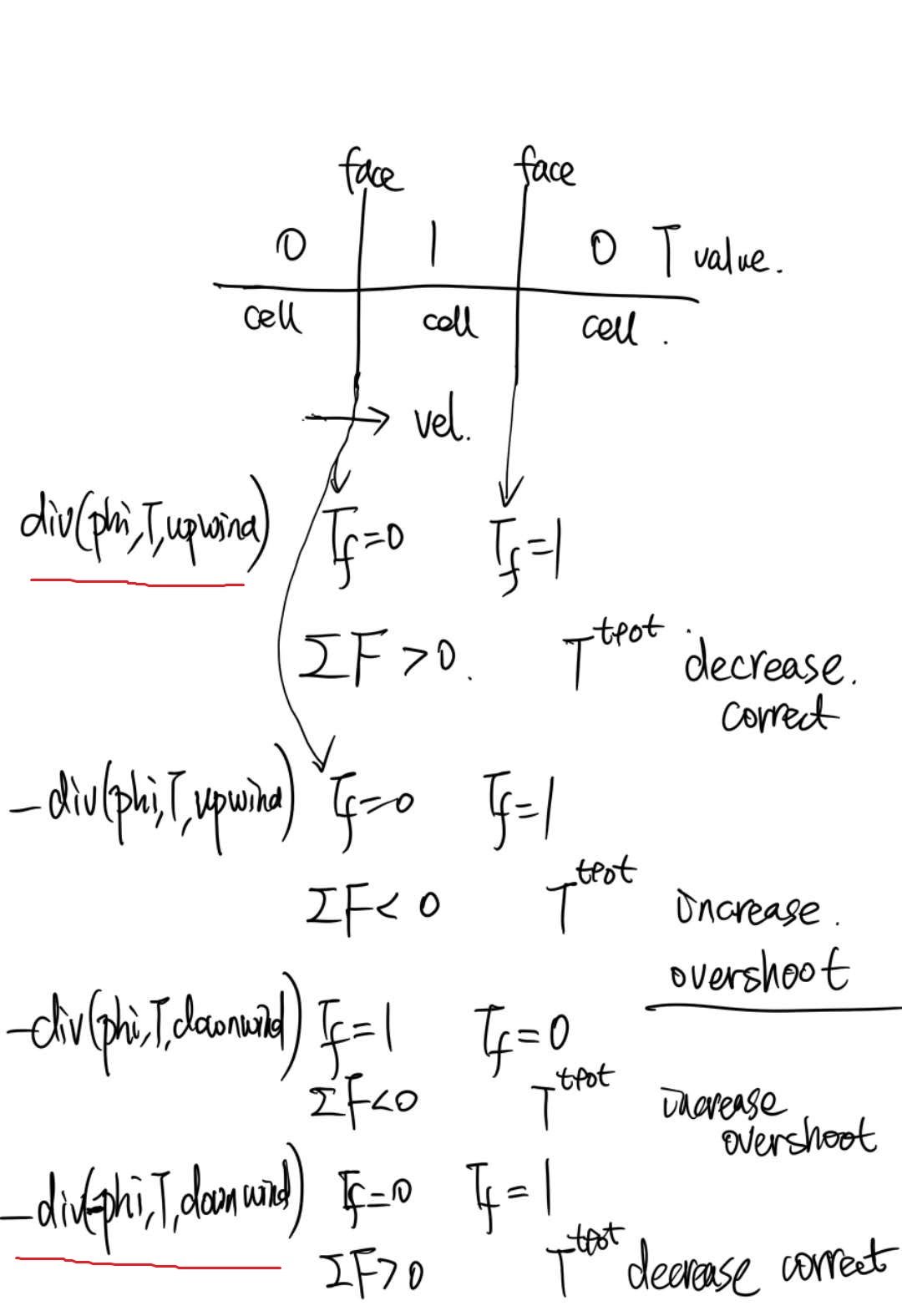
-div(phi,T) 和div(-phi,T)结果为何不同?

[Mr.H]

各位前辈，我在做拓扑优化，里面求解伴随温度的方程如下：

fvScalarMatrix TtEqn
(
    fvm::div(-phi,Tt)
  + Tt*fvc::div(-U)
  + fvm::laplacian(-ka,Tt)
);

TtEqn.relax();
TtEqn.solve();

Tt 在inlet 和wall 是fixedValue 0，在outlet是定制的边界条件，通过计算得到。
结算结果在靠近inlet第一层网格莫名升高，如下图：

如果把 div(-phi,T)换成 -div(phi,T)，会出现栅格分布，如下图：

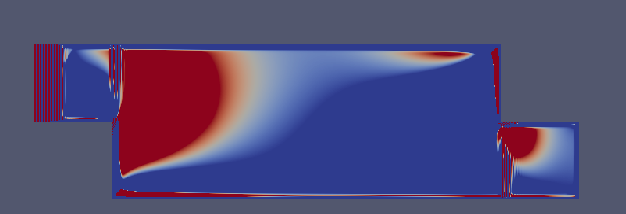
貌似div(-phi,T)是从下有获得信息，逐步向前更新，-div(phi,T)是从上有更新信息。
为何结果会如此不同？

[李东岳]

貌似div(-phi,T)是从下游获得信息，逐步向前更新，-div(phi,T)是从上有更新信息。

你理解的非常正确。你应该是用了迎风格式。div(-phi,T)+迎风等于下风格式，是从下游获取信息。-div(phi,T)就是减去上游的信息。下风格式压缩性非常厉害，过分的使用会导致非常不稳定。

[Mr.H]

@东岳 改成了下面的方程，div(phi,T)采用Gauss upwind格式

fvScalarMatrix TtEqn
(
    fvm::div(phi,Tt)
  + Tt*fvc::div(U)
  + fvm::laplacian(ka,Tt)
);

TtEqn.relax();
TtEqn.solve();

计算结果如下：

的确是从inlet开始更新，但在从壁面开始出现了严重的震荡，什么样的格式会好一些？

[李东岳]

$$\begin{array}{}\text{(1)}& \mathrm{\nabla }\cdot (\mathbf{U}T)+T\mathrm{\nabla }\cdot \mathbf{U}+\mathrm{\nabla }\cdot (k\mathrm{\nabla }T)\end{array}$$
解这个方程？你这个瞬态稳态？

[Mr.H]

@东岳 对是这个方程，稳态。inlet 和wall 都是fixed value 为 0。
出口边界条件是，Tu∙n+k∇T∙n-u_n=0，我单独编写了一个出口的边界条件。

[李东岳]

方程3的第二项可以删掉么？

[Mr.H]

@东岳 可以删掉，这一项本来为零，疏漏了。 删掉后结果一样，在壁面处有剧烈震荡。 相对于一般温度方程，导热项前面是 “+”。

[李东岳]

你植入在了simpleFoam里面？

[Mr.H]

@东岳 对，我植入在simpleFoam 里面，增加了一个TEqn.H的头文件

[李东岳]

fvScalarMatrix TEqn
			(
				fvm::div(phi, T)
			  - fvm::laplacian(Tnu, T)
			);

			TEqn.relax();
			TEqn.solve();

我加了一下，没有任何问题？你是要植入上面的方程吧？

[CambridgeARDC]

楼主你好，我也准备用OpenFOAM做拓扑优化，请问可以指导与交流一下吗？谢谢

[李东岳]

这是div(phi,T)与-div(phi,T)等的解释