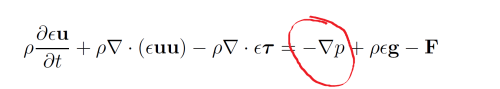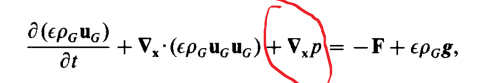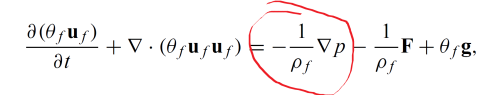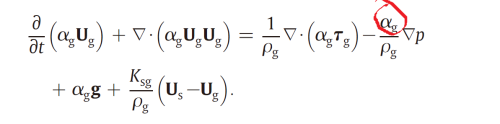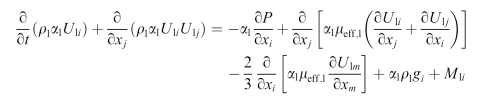欧拉及拉格朗日下的动量方程压力项竟然不一样
-
昨天在植入算法的时候（参考多相流的数学模型里面的方程），发现最后推导出来的压力泊松方程里面带一个$\alpha_\rc^2$ 。之前从来没见过带平方的压力泊松方程
于是回头仔细仔细再仔细的看方程，看是不是哪里错了。到头来，发现最开始的连续相动量方程文献里面竟然不一样，就是上文说的，压力梯度项相差一个相分数$\alpha_\mathrm{c}^2$。此处不赘述。昨晚上搞完之后就出去喝酒了。现整理思路，总结一下。
欧拉欧拉以及欧拉拉格朗日下连续相方程的压力梯度项区别
现在把俩种形式的方程写一下，欧拉欧拉下连续相方程A：
\begin{equation}\label{A}
\frac{{\p \left( {{\alpha_\rc}{\bfU_\rc}} \right)}}{{\p t}} + \nabla \cdot \left( {{\alpha_\rc}\left( {{\bfU_\rc} \otimes {\bfU_\rc}} \right)} \right) - \nabla \cdot \left( {{{\alpha_\rc}}{\bfR_\rc}} \right)
=-{\color{red}{\alpha_\rc}} \nabla\frac{p_\rc}{\rho_\rc} + \alpha_\rc\bfg - \bfM_\rd.
\end{equation}欧拉拉格朗日下连续相方程B：
\begin{equation}\label{B}
\frac{{\p \left( {{\alpha_\rc}{\bfU_\rc}} \right)}}{{\p t}} + \nabla \cdot \left( {{\alpha_\rc}\left( {{\bfU_\rc} \otimes {\bfU_\rc}} \right)} \right) - \nabla \cdot \left( {{\alpha_\rc}{\bfR_\rc}} \right)
=-\nabla\frac{p_\rc}{\rho_\rc} + {\alpha_\rc}\bfg - \bfM_\rd.
\end{equation}方程\eqref{A}和\eqref{B}的区别在于一个$\alpha$。文中符号含义请参考多相流的数学模型，此略。
这个区别大么？
目前并不清楚。但很明确的是，从方程\eqref{A}最后推导出来的压力泊松方程为：
\begin{equation}
\frac{\p \alpha_\rc}{\p t}+\nabla_\bfx\cdot\left(\alpha_\rc\left(\mathbf{Pre}+\mathbf{HbyA}\right)\right)=\nabla_\bfx\cdot\left(\frac{\alpha_{\rc}^{\color{red}2}}{A_{\mathrm{P}}}\nabla \frac{p_\rc}{\rho_\rc}\right).
\label{pressureB}
\end{equation}
从方程\eqref{B}最后推导出来的压力泊松方程为：\begin{equation}
\frac{\p \alpha_\rc}{\p t}+\nabla_\bfx\cdot\left(\alpha_\rc\left(\mathbf{Pre}+\mathbf{HbyA}\right)\right)=\nabla_\bfx\cdot\left(\frac{\alpha_{\rc}}{A_{\mathrm{P}}}\nabla \frac{p_\rc}{\rho_\rc}\right).
\label{pressureA}
\end{equation}在写代码的时候，分别对应俩种形式：
fvScalarMatrix pEqn ( fvm::laplacian(alphacf*rAUcf, p) == fvc::ddt(alphac) + fvc::div(alphacf*phiHbyA) );fvScalarMatrix pEqn ( fvm::laplacian(alphacf的平方*rAUcf, p) == fvc::ddt(alphac) + fvc::div(alphacf*phiHbyA) );为什么？
并不知晓。昨天把本帖随手发了个朋友圈，下面这个朋友的评论非常在理
自古高手在朋友圈啊
but why? 接下来，只能从物理的角度来推方程了。首先，我们要考虑颗粒的大小：
- 大颗粒：颗粒体积相对网格单元体积较大，或者数量众多，导致不能忽略，即$\alpha_\rd\neq 0$
- 小颗粒：反之，$\alpha_\rd\approx 0$
然后，除了颗粒的受力，除了曳力（阻力）外，我们主要考虑颗粒所受的压力梯度，如下图中的$\nabla p$。
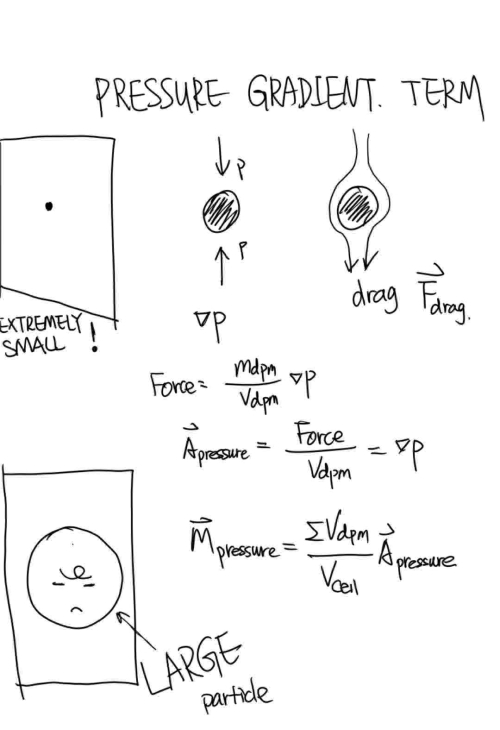
最后，我们的压力梯度交换项就是图中的$\bfM_{\mathrm{pressure}}$。$\bfM_{\mathrm{pressure}}$的值就是导致带相分数或者不带相分数的区别。
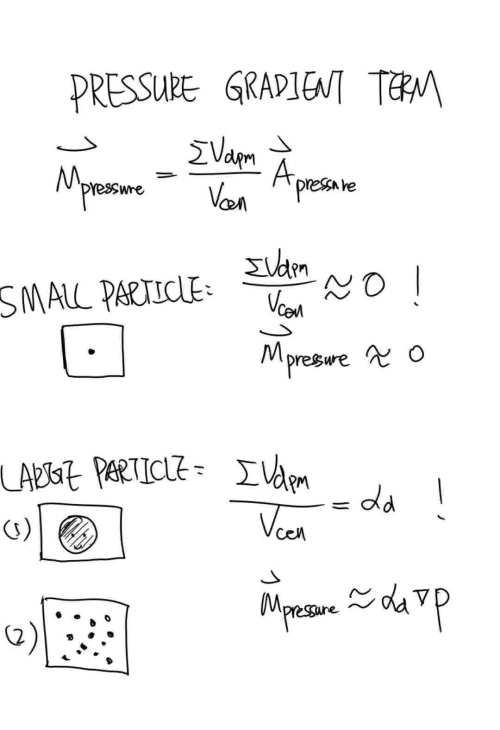
考虑大颗粒小颗粒俩种情况，如下图：
- 对于小颗粒，$\alpha_\rd\approx 0$导致$\bfM_{\mathrm{pressure}}\approx 0$
- 对于大颗粒或者颗粒群，$\bfM_{\mathrm{pressure}}\approx - \alpha_\rd \nabla p$（图中忘记了一个负号）
好了，重新考虑方程\eqref{B}中右边的压力项有（$\rho_\rc=1$）：
\begin{equation}
-\nabla p_\rc - \bfM_\rd = -\nabla p_\rc + \alpha_\rd \nabla p_\rc = -\alpha_\rd \nabla p_\rc
\end{equation}
这样，方程\eqref{A}和方程eqref{B}就相符了。结论
方程\eqref{A}和方程\eqref{B}的区别就在于考没考虑粒子的压力梯度项：
- %(#ff0000)[考虑粒子的压力梯度，则有相分数，对应方程]\eqref{A}
- %(#ff0000)[没考虑粒子的压力梯度，则没有相分数，对应方程]\eqref{B}
我在好多论文里面看到直接给出方程\eqref{A}和方程\eqref{B}，没有一点解释。是太过基础了么？总之，现在我明白了。
（虽然英文图，但我自己画的）
