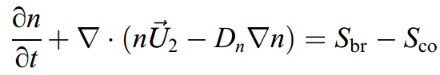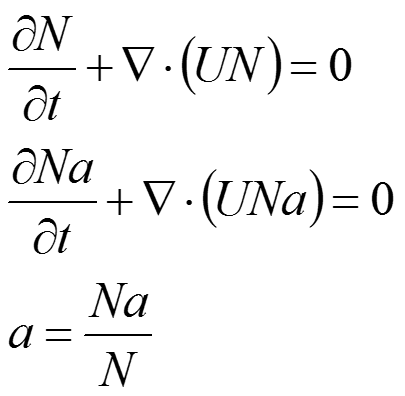自己写的一个空化求解器的气泡数，气泡质量，气泡半径和气泡半径速度的守恒方程的一些疑问

[100yearsalone]

大家好，我一直是在基于rhoPimpleFOAM去做一个空化的求解器。

基本思路是;
自己写的空化求解代码 -> rhoPimpleFOAM的代码 -> 自己定义的各个量在网格的守恒方程

从第一步的空化求解代码得到四个自定义的值，分别是气泡数，气泡质量，气泡半径和气泡半径速度。

气泡质量 单位kg/m3

气泡数 单位1/m3

气泡半径 实际上是半径乘数量 单位 1/m2

气泡半径速度 实际上是半径速度乘数量 单位 1/m2s

以上四个就是自定义量的守恒方程，用以计算在格子中生成后，跟随流动的变化。
其中自定义通量phit1和密度rhot的定义分别为

在creatfieds处定义了rhot，然后在0文件夹中见了一个rhot文件作如下设置：

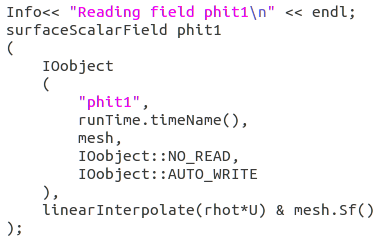
在creatfields中定义了phit1，我是仿照通量phi去写的

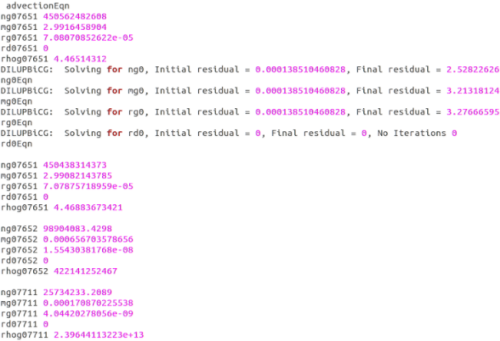
我自己简单的试了一下好像可以，但是在真的运算中气泡数缺出现了负值如图

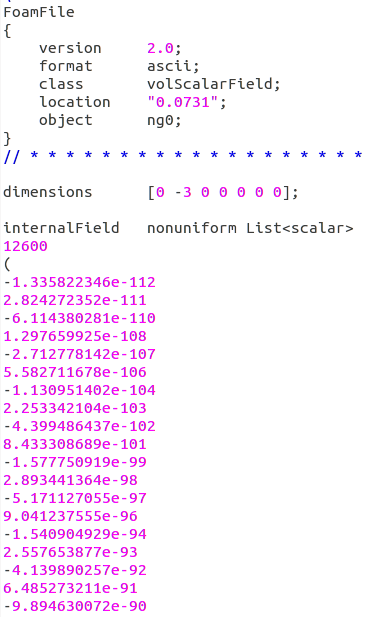
不知各位有没有类似定义过守恒方程经验的同学能够提供点意见？

[mohui]

@100yearsalone 我也是做空化这方面的，我有个问题想确认下，rhopimplefoam是基于密度基写的方程，请问你是如何引入两相流进去的呢？难道类似与正压模型那样，最后基于密度得到alpha分布吗？

[100yearsalone]

@mohui
我是在自己写的空化代码中求 Rayleigh–Plesset 方程，得出气相的数据和气体和液体alpha。把原方程求的rho当成混合流的密度来看，再求出液相的密度。

[yhdthu]

界面不用处理？

[100yearsalone]

@yhdthu 没处理

[mohui]

@100yearsalone 恩，看了你的代码，感觉很奇怪的一点是，你的气泡数，气泡质量，气泡半径和气泡半径速度参数的输运方程本身有意义吗？能给出详细的推导过程，我看了看，初步看不出来你所建的输运方程的合理性。

[李东岳]

你需要群体平衡模型来描述气泡相关的东西。你自己写的这个标量传输方程很简单，气泡数，气泡质量，气泡半径和气泡半径速度这些并不能够单纯的考虑成为标量传输。

个人思路：

1. 气泡数量密度，你可以写为（跟你那个差不多）
   \begin{equation}
   \frac{\partial N}{\partial t}+\nabla\cdot(\mathbf{U}N)=0
   \end{equation}
   上述方程你没有考虑任何成核、结晶、蒸发等。也就是说你的气泡总数是不变化。
2. 气泡质量你不需要传输方程。
3. 气泡半径不存在传输方程，如果你不考虑气泡破碎等间断性变化等，气泡半径只能是连续性变化，只需要用理想气体状态方程计算就可以，因为在上面的方程中你没有考虑其他气泡产生和消失项。
4. 气泡半径速度是什么？

另外，rhoPimpleFoam是单相求解器，基于这个求解器写方程是单向耦合。多向耦合你需要多向求解器。

我建议你参考群体平衡模型理论。如果你觉得很复杂，可以参考简化版：

Predicting gas–liquid flow in a mechanically stirred tank

不要考虑应用工况（如stirred tank），在这篇文章中，方程12就是你的气泡数量，但是同时考虑了气泡的破碎聚并。相对来说模型已经完善了，你直接植入进去就行。我写的方程1就是不存在扩散、不存在一、二阶动力学的情况。上述文献请只参考section 4。

[100yearsalone]

@李东岳
你好，李老师
我目前就想试试气泡数量密度的传输方程，我试了几个进行了测试。

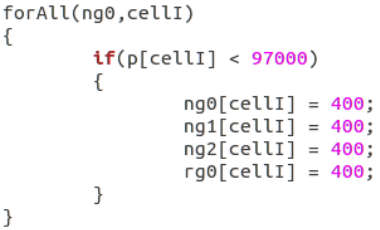
你的回答公式无法正式显示，所以我自己查了一下这样定义了。


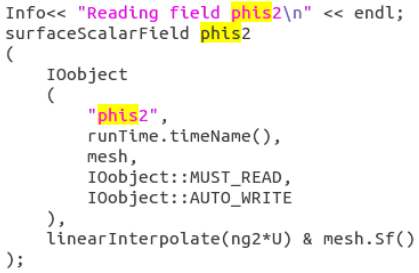
其中ng2是气泡数量密度，phis2是通量，我感觉应该是没问题的，但是实际运行后结果是
ng2没有发生移动。
我试了一下另外两种定义rg0和rg1，phis0=rhog0U，phis1=rhoU

成功流动，结果一样


rhog和rho

rho和rhog不一样，结果是一样，代表我以后传输方程只用随便定义一个密度是吗？如果不是的话，为什么一开始的式子没发生流动呢？

[李东岳]

你开始的代码

fvm::ddt() + fvc::div(phis2)

里面你只是定义了phis2，并没有更新phis2，因此这个值每个时间步不变所以没有移动。你需要在每个时间步里面计算一下:

while(TIMELOOP)
{
    phis2 = phi*fvc::interpolate(s2);
}

[100yearsalone]

@李东岳
我按照你给我那篇论文里的式子

不含有扩散项和源项

其中mg21就是气泡数量密度，上面的phis2是通量

气泡个数发生的测试条件是这样，我觉得我设置得没有什么问题，但是有一点不太明白

就是在结果里面为什么会出现负值？

[李东岳]

forAll是做什么的？

[100yearsalone]

@李东岳
读取每个cell的值

[李东岳]

结果越界了，用迎风试试

[100yearsalone]

@李东岳
老师，您之前给我写了一个气泡数量密度的运输方程是图中的第一个式子

对于有些标量，例如a我想跟随这个N做移动，我设另外一个标量N乘以a等于Na做同一样的运输方程，如图中式子2
求完N和Na以后，再相除求出a，这种方法在OF里面应该是没问题的吧？
我试了一下，好像不太符合我的预期。
我设了ng0作为第一个式子的N，得出下图：

而rg0作为a，a为常值1，ngrd的结果：

我很不解为什么ngrd的运输方程计算后会出现这种结果？

[李东岳]

例如a我想跟随这个N做移动，我设另外一个标量N乘以a等于Na做同一样的运输方程，如图中式子2

不理解你这句话。另外你上面三个图实际上是完全一样的方程。为什么要求解三个？

ngrd是什么？

[100yearsalone]

@李东岳
ngrd就是两个标量的乘积，第一个式子求了ng，第二个式子求ngrd，最后相除得rd
不过听您这么一说我可能又想错了

这图上面ng0是气泡数，mg0是气泡质量，rg0是气泡半径，rhog0是根据这三个计算的密度。
在运输之前只有一个格子有值，运行运输方程后变成三个格子有值了，可是从密度来看另外两个格子都变成了极大的数，
我就是找个方法比较稳定的传输这几个值，让他们运输以后不偏差密度值太多。

[李东岳]

提示一点：如果求解本身不符合物理的传输方程，结果肯定是不复合物理。

[LiuZhuang]

@100yearsalone 新写的phit1里的U，这个U是从0文件夹下的U调用的么？