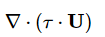代码实现?
-
@李东岳 请问tau如下定义可以吗?
volTensorField tau("tau", muEff*(dev2(gradU.T()) + gradU));因为
\begin{equation}
dev2((\nabla u)^{T})=(\nabla u)^{T} - \frac{2}{3}tr((\nabla u)^{T})I = (\nabla u)^{T} - \frac{2}{3}(\nabla . u) I
\end{equation}
所以
\begin{equation}
\tau = \mu (dev2((\nabla u)^T) + \nabla u)
\end{equation} -
@程迪
谢谢!看rhoCentralFoam时没看懂,看了你的链接清楚一些了。
我主要是想在能量方程中添加$\nabla \cdot(\tau \cdot u)$,然后计算耗散函数$\tau:(\frac12(\nabla u + (\nabla u)^T))$。
根据CFD中的能量方程,$\nabla \cdot(\tau \cdot u)$好像没法展开成可以隐式离散的项。
看rhoCentralFoam中的能量方程,除时间项外,用的都是显式离散。所以,对于能量方程来说,是不是不必拆项并使用隐式格式?
至于动量方程中的$\nabla \cdot \tau$,对于一般的求解器,应该是包含在UEqn.H里的turbulence->divDevRhoReff(U)吧,不用我们自己定义。rhoCentralFoam中的能量方程:
surfaceScalarField sigmaDotU ( "sigmaDotU", ( fvc::interpolate(muEff)*mesh.magSf()*fvc::snGrad(U) + fvc::dotInterpolate(mesh.Sf(), tauMC) ) & (a_pos*U_pos + a_neg*U_neg) ); solve ( fvm::ddt(rhoE) + fvc::div(phiEp) - fvc::div(sigmaDotU) ); -
@程迪
rhoE应该是$\frac{\partial \rho e}{\partial t} + \frac{\partial \rho K}{\partial t}$
phiEp应该是$\nabla \cdot (\rho \mathbf{U} e)+\nabla \cdot (\rho \mathbf{U} K)+\nabla\cdot(p\mathbf{U})$
sigmaDotU应该是$\nabla \cdot(\tau \cdot \mathbf{U})$
感觉拆不了。另外,请问对定常的求解器也有时间步限制吗?如果没有的话,是不是定常的求解器中,比如buoyanySimpleFoam,就不用管隐式还是显式了?

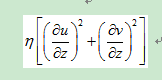 图中的式子,我想加在能量方程里,代码该怎么实现?(我还是一个编程菜鸟,不太会编程,希望有人可以帮我一下)
图中的式子,我想加在能量方程里,代码该怎么实现?(我还是一个编程菜鸟,不太会编程,希望有人可以帮我一下)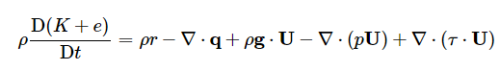 这个公式里的最后一项应该是粘性耗散热吧?如果用这个编程
这个公式里的最后一项应该是粘性耗散热吧?如果用这个编程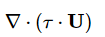 ,该怎么实现呢?是不是和这一项是一致的?
,该怎么实现呢?是不是和这一项是一致的?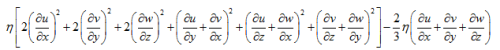 我研究的模型中,速度在x和y方向的变化很小,忽略以后就是那样的了。(东岳老师给的链接页面不存在了)
我研究的模型中,速度在x和y方向的变化很小,忽略以后就是那样的了。(东岳老师给的链接页面不存在了)