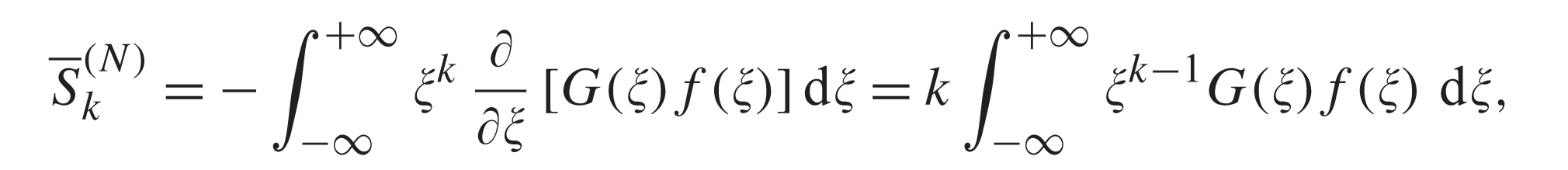一个积分
-
\begin{equation}
-\int r^k \frac{\mathrm{d}}{\mathrm{d}r}\left( \phi ( r ) f( r ) \right) \mathrm{d} r =
\end{equation}
文献里面这么给的
\begin{equation}
-\int r^k \frac{\mathrm{d}}{\mathrm{d}r}\left( \phi ( r ) f( r ) \right) \mathrm{d} r = \int k r^{k-1} \phi ( r ) f ( r ) \mathrm{d} r
\end{equation}
这事我算的：
\begin{equation}
-\int r^k \frac{\mathrm{d}}{\mathrm{d}r}\left( \phi ( r ) f( r ) \right) \mathrm{d} r = -\int r^k \mathrm{d} \left[ \phi( r ) f ( r ) \right]=-\left(r^k \phi( r ) f ( r ) - \int \phi( r ) f ( r ) \mathrm{d} r^k \right)=-r^k \phi( r ) f ( r ) + k \int r^{k-1} \phi( r ) f ( r ) \mathrm{d} r
\end{equation}
后面怎么多出来这个项：$-r^k \phi( r ) f ( r ) $? -
这个是文献里面的。怎么回事呢。
-
推导的时候忘记了积分限。添加积分限之后则和文献一致。如图：
-
$\frac{\partial \left( \int v^kn(v)\mathrm{d}d \right)}{\partial v}$ does not equal to $\int v^k\frac{\partial n(v)}{\partial v}\mathrm{d}d$
-
find . -type f | xargs -n 5 touch
