有意思的CFD算法类研究
-
概述:大量的工业过程中如化工反应器、环境沙尘流动、沉降现象、流化床鼓泡床、交通流、空化现象等都可以使用CFD的多相流模型进行预测。多相流算法远比单相流复杂的多,单相流的研究重点,只是多相流的研究的一个方面。下面仅举2个例子
-
对于单相流中的湍流模型封闭问题,在多相流中依然存在。同时,多相流还需要附加考虑相间湍流作用。比如比较著名的Bubble induced turbulence现象;
-
对于单相流中的DNS模拟问题,在多相流中依然存在。同时,多相流模型还需要附加考虑相界面的尖锐程度、有界性等数值内容;
多相流研究领域目前远没有单相流模型成熟。多相流模型框架如下图所示(微信里不显示图,可以点击右上角在浏览器中打开),个人感兴趣的主要为下图中的
Eulerian-Eulerian欧拉欧拉模型,Eulerian-lagrangian欧拉拉格朗日模型,Eulerian-QBMM欧拉QBMM模型,以及一些其他模型。本帖列举一些个人的科研过程中,思考的一些有意思的研究方向。个人精力有限,相关研究方向仅仅列出具体内容,当然也具有工业意义和背景,参考文献也应该给出。但都从略不写,比较费时。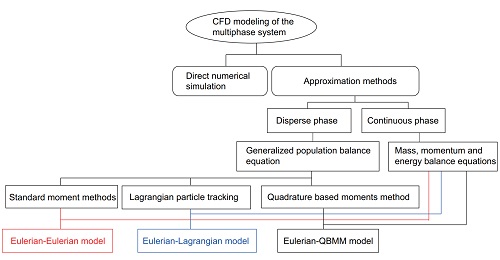
欧拉欧拉模型的研究
欧拉欧拉模型复杂, 如何在有限体积法框架下获得合理的解依然是学术界一个热门话题,目前国际上的CFD大厂也持续的对所植入的欧拉欧拉算法进行优化。
-
求解相方程的FCT框架下的高阶算法相分数的有界属于TFM求解中的经典问题,选择不合适的数值结构会引起相分数的越界。相分数的越界一方面表明了相分数的结果不符合物理,另一方面导致界面传递模型不可计算。
目前CFX中采取的数值操作主要为基于TVD框架的高阶格式,目前在OpenFOAM中采取的数值操作主要为基于FCT的通量限制算法(MULES),然而至今依然存在缺陷且在某些情况下会引起相分数的越界。
在OpenFOAM中植入一种低耗散的高阶的稳定的同时可保证相分数有界的算法的研究和验证将会对CFD中求解TFM数值求解领域具有一定的贡献。
-
同位网格上多相流的体积力无振荡处理虽然欧拉欧拉模型结构紧凑,但是欧拉欧拉模型合理的数值求解依然具有一定的挑战性。具体体现在如相转置带来的界面传递模型不符物理、相分离情况下的方程组奇异问题、Rhie-Chow插值下的无震荡体积力处理、非正交网格下的数值稳定性问题。尤其在同位网格下,不合理的处理体积力会导致震荡解。例如对于简单的单相流震荡现象:http://www.cfd-china.com/topic/746 对于多相流中依然存在震荡问题。
在OpenFOAM中针对现存非守恒、半守恒、全守恒的TFM模型,植入一种无震荡的速度压力耦合算法,可以对CFD,尤其是TFM数值求解领域具有一定的贡献。
-
一种多相流速度压力耦合以及时间离散格式目前TFM中压力均为求解静压方程获得,然而这对于密度比较大的液体存在一定的收敛问题,参考OpenFOAM中的VOF模型,双流体模型的压力方程也可以采用类似的方法进行重构来提高收敛性。
同时,现存CFD算法为了保证TFM求解的稳定性,均采用一定的数值手段保证求解稳定性,大部分的操作体现在通过曳力耦合不同相的速度。但是现存的方法均为采用的一种假稳态的思路,这对于密度比较大的气固流动并不适用。类似这种问题可以通过重新对TFM采用一种操作符切分(Operator Splitting)的思想进行求解来体现耦合的渐变性。
在OpenFOAM中植入一种真正瞬态的多相流速度压力耦合以及时间离散格式,可以对TFM数值求解领域,尤其是TFM在气固模拟领域的应用具有一定的贡献。
-
isoAdvector算法、界面压缩算法在欧拉欧拉模型中的植入和应用isoAdvector为2016年Roenby et al. 提出的一种计算相分数的数值算法,目前已经应用在VOF模型中并用于计算较大相界面的多相问题。目前TFM模型中算法对于非结构网格收敛性较差,isoAdvector则在非结构网格中依然可以保持非常高的界面重构且数值耗散较低。同时,isoAdvector作为一个全新的数值求解思想,依然需要大量的优化以及验证研究。另一种可能的算法为在欧拉欧拉模型的动量方程中植入一个界面压缩项,该项使得原本不具备明晰相界面的欧拉欧拉模型的相界面变得更加尖锐。
目前,研究isoAdvector和双流体模型结合的可能、以及在欧拉欧拉模型的界面压缩项的植入,是一个具有一定创新性的研究方向。
欧拉拉格朗日模型的研究
-
粒子跟踪的重心算法欧拉拉格朗日模型作为介尺度模型,可以预测欧拉欧拉模型无法预测的内容。其牺牲的为计算资源。对于大量颗粒的模拟,欧拉拉格朗日需要高效有效的粒子跟踪算法,需要能做到非全局循环、不丢失、且粒子不会被trap,之前的OpenFOAM中植入的粒子跟踪算法起源于分子动力学模拟。但在偶然的非常特殊的情况下,会导致粒子丢失和trap。这往往在网格畸变严重的时候发生。
粒子的丢失会导致质量不守恒,更严重的粒子trap现象导致计算无法进行。William在新版本的OpenFOAM中植入了新的粒子跟踪算法,相对于旧版本的粒子跟踪算法,尽可能的避免了粒子丢失和trap现象。该算法已经被植入OpenFOAM,但如要系统的自算法层面的研究和验证。
这种高效的无粒子丢失和trap的粒子跟踪算法,对欧拉拉格朗日、分子动力学模拟求解领域具有一定的贡献。
-
拉格朗日粒子界面力耦合源项以及ODE算法验证在更新拉格朗日粒子方程的时候,需要求解拉格朗日粒子的ODE方程。目前可调用的时间格式主要有欧拉隐形、欧拉显性等。经过一些算例的验证,ODE方程的算法稳定性和时间格式以及界面力的处理直接相关。例如,在仅仅考虑重力显性源项的时候,采用ODE的精确解预测下一个时间步的速度误差较大,随着时间的累积误差会进一步积累。
针对拉格朗日粒子ODE方程的时间格式以及界面力耦合源项的处理方式关系研究将建立普适性的准则。
Eulerian-QBMM的研究
PBM中文译名为群体平衡模型,GPBE中文译名普适性群体平衡模型,是从统计学角度来表述粒子分布演变的偏微分方程,GPBE也被称之为玻尔兹曼方程等。注意PBM并不同于GPBE。
\begin{equation}
\frac{\partial n}{\partial t}+\frac{\partial \mathbf{U}}{\partial \mathbf{x}}+\frac{\partial \mathbf{A}}{\partial \mathbf{U}} = \mathrm{S}
\end{equation}
GPBE主要用于粒子(颗粒或者气泡)统计学方面的预测,如平均(局部)粒子直径,平均(局部)粒子速度、传质系数等。目前PBM已经成功的和大量的工业过程结合进行预测,如反应器内的传质预测、流化床鼓泡床等多相混合的粒子特性预测、发动机喷雾、引擎燃烧、雾霾模拟、溶质结晶增长等。PBM研究的难点在于方程难于求解以及和CFD的耦合验证。PBM目前的求解方法主要有类方法(Class Method),矩方法(Quadrature-Based Method of Moments),加权参数法(Weighted Residual Method)等。各个方法有分属不同的自方法,如类方法下分属非均一类方法(Inhomogeneous Class Method)、均一类方法(Homogeneous Class Method),以及各种变种等。矩方法分为拓展矩方法(Extended QMOM)、条件矩方法(CQMOM)等。PBM可单独求解,也可作为CFD外挂模型求解(类似CFD-DEM)。-
基于通量分裂思想的矩传输算法在使用矩方法进行PBM或GPBE的求解时,保证矩的可实现性为算法的关键。在有限体积法中,目前只有一阶精度(附加一定量的数值耗散)才能保证矩的可实现性。Vikas et al. 在2013年提出了一种基于通量分裂算法的有效的高阶格式。Laurent and Nguyen在2017年提出了zeta、QW算法也可以保证矩传输的可实现性。
然而,上述方法虽然可以保证矩的可实现性,但并不能保证矩的有界性。如何基于可实现算法,进一步保证矩的有界性,是将PBM用于工业应用的一大障碍。
-
一种无均一速度假定的CFD-PBM算法在鼓泡床中的验证对比在OpenFOAM中植入相关的算法并用于鼓泡床工况模拟并和实验对比对化学工程领域具有一定的贡献。
-
气液流动中的气泡界面传输方程和PBM的验证对比在OpenFOAM中对气泡界面传输方程和PBM在气液流动中的模拟结果和实验结果进行对比对化学工程领域具有一定的贡献。
其他
-
R13方程在OpenFOAM中的植入以及多相流验证在部分情况下,N-S方程是失效的。比较典型的情况为稀薄气体。鉴定N-S方程是否失效的有限方法为判断系统的Kn数,已有文献表明在Kn数大于0.05的时候,就不能继续使用N-S方程对系统进行描述。在这种情况下,需要采用普适性群体平衡模型、也即玻尔兹曼方程进行求解预测。直接求解玻尔兹曼方程基本是不可能的。在稀薄气体研究领域,基于矩方法的R13方程是一种有效途径。
同样,在气固多相流领域,基于欧拉框架下的方程并不能够预测某些行为如颗粒轨迹交叉。鉴于R13方程在稀薄气体领域的成功应用,将R13方程用于气固多相流领域是一个具有一定创新性的研究领域。
-

 资料以后会持续更新,精力有限,稍微慢点
资料以后会持续更新,精力有限,稍微慢点