基于hPolynomial热物理模型实现Cp多段多项式拟合过程中遇到的问题
-
遇到的问题：
依照hPolynomial的结构和想法，改动之后应该能实现多段拟合，而事实是并不能。发生了一件很奇怪的事：
假定Cp1在温度区间120～150K拟合，Cp2在温度150～180K拟合，当给算例的温度T初始边界条件在120～150K任意区间能正常求解。同样给定算例的温度T初始边界条件在150～180K任意区间也能正常求解。但是给定120～180K的跨温度区间就无法求解，一般求解几步就会报"Maximum number of iterations exceeded"的错误。对温度求解进行分析后发现：
在温度求解的地方输出：Info << "Test=" << Test << " Tnew=" << Tnew << " F=" << (this->*F)(p, Test) << " f=" << f << " Cp=" << (this->*dFdT)(p, Test) << endl;其中有不少的地方出现了异常的温度（初始场温度为130K，加热壁面为170K）：
Test=130 Tnew=130 Test=129.997 Tnew=129.991 F=-1.24552e+06 f=-1.24554e+06 Cp=3534.94 Test=129.997 Tnew=129.991 Test=129.885 Tnew=129.697 F=-1.24591e+06 f=-1.24658e+06 Cp=3534 Test=129.697 Tnew=129.697 F=-1.24658e+06 f=-1.24658e+06 Cp=3532.43 Test=129.697 Tnew=129.697 est=124.7 Tnew=119.789 F=-1.26413e+06 f=-1.28129e+06 Cp=3494.07 Test=119.789 Tnew=119.765 F=-1.28121e+06 f=-1.28129e+06 Cp=3461.82 Test=119.765 Tnew=119.765 F=-1.28129e+06 f=-1.28129e+06 Cp=3461.68 Test=119.765 Tnew=119.765 Test=130 Tnew=130 F=-1.24551e+06 f=-1.24551e+06 Cp=3534.96很快，这些地方求解温度就会出现严重问题而发散：
Test=130 Tnew=129.999 F=-1.24551e+06 f=-1.24551e+06 Cp=3534.96 Test=130 Tnew=129.999 Test=129.995 Tnew=129.993 F=-1.24553e+06 f=-1.24553e+06 Cp=3534.92 Test=129.995 Tnew=129.993 Test=129.949 Tnew=129.937 F=-1.24569e+06 f=-1.24573e+06 Cp=3534.53 Test=129.949 Tnew=129.937 Test=129.539 Tnew=129.469 F=-1.24714e+06 f=-1.24739e+06 Cp=3531.12 Test=129.469 Tnew=129.469 F=-1.24739e+06 f=-1.24739e+06 Cp=3530.54 Test=129.469 Tnew=129.469 Test=126.311 Tnew=125.995 F=-1.25849e+06 f=-1.2596e+06 Cp=3505.78 Test=125.995 Tnew=125.995 F=-1.2596e+06 f=-1.2596e+06 Cp=3503.43 Test=125.995 Tnew=125.995 Test=100.516 Tnew=99.569 F=-1.34695e+06 f=-1.35014e+06 Cp=3365.81 Test=99.569 Tnew=-144277 F=9.35162 f=-1.35014e+06 Cp=9.35162 Test=-144277 Tnew=-288653 F=9.35162 f=-1.35014e+06 Cp=9.35162 Test=-288653 Tnew=-433029 F=9.35162 f=-1.35014e+06 Cp=9.35162 Test=-433029 Tnew=-577405 F=9.35162 f=-1.35014e+06 Cp=9.35162 Test=-577405 Tnew=-721781 F=9.35162 f=-1.35014e+06 Cp=9.35162到目前为止我还未找到这个问题的原因，所以来请教大家，希望高手能指点一二，在此表示非常感谢！
相关信息描述
OF中hPolynomial热物理模型（位置在src/thermophysicalModels/specie/thermo/hPolynomial/）是利用温度T对Cp(T)进行多项式拟合，默认只能拟合一段。
但是，在一些超临界的状态下，Cp随温度的变化会变化剧烈，如下图：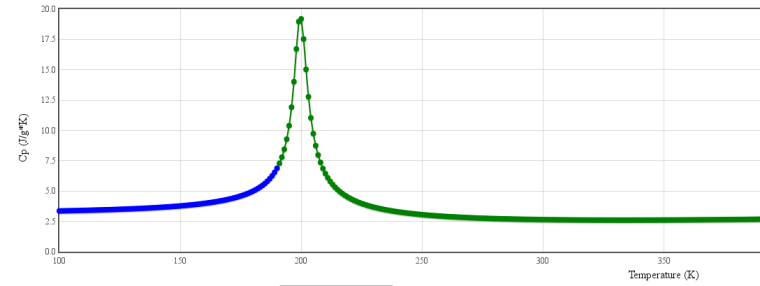
对于这样的状态进行一段拟合显然是不够的。而janaf热物理模型是基于NASA的JANAF表来拟合，表的数据是常压下的，而且其系数前5个虽然可以确定，但是后两个参数目前我还没找到是如何计算的，与此同时，它也只能分为两段。所以基于hPolynomial热物理模型还是比较靠谱的。依据对hPolynomial原有的结构进行模仿：
hPolynomialThermo.H（这个是对私有成员的定义）：
改动后：
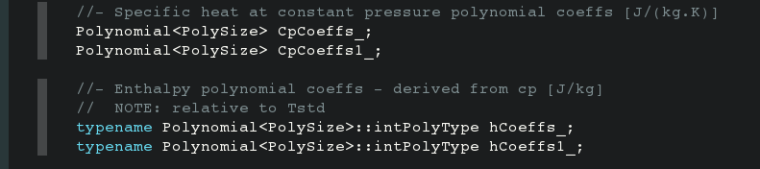
hPolynomialThermo.C（这个主要是对构造函数的改动，它从算例的constant/thermophysicalProperties中的子字典thermodynamics读取拟合的Cp系数。例如：
thermodynamics { // *** hPolynomial // Cp = [J/kg/K] Hf 0; Sf 0; CpCoeffs<8> (1282.86457 52.95551 -0.47949 0.00158 0.0E+00 0.0E+00 0.0E+00 0.0E+00);// Cp(T) CpCoeffs1<8> (-114079.86247 2265.15184 -14.63133 0.03179 0.0E-07 0.0E-07 0.0E-11 0.0E-15); }
改动后：
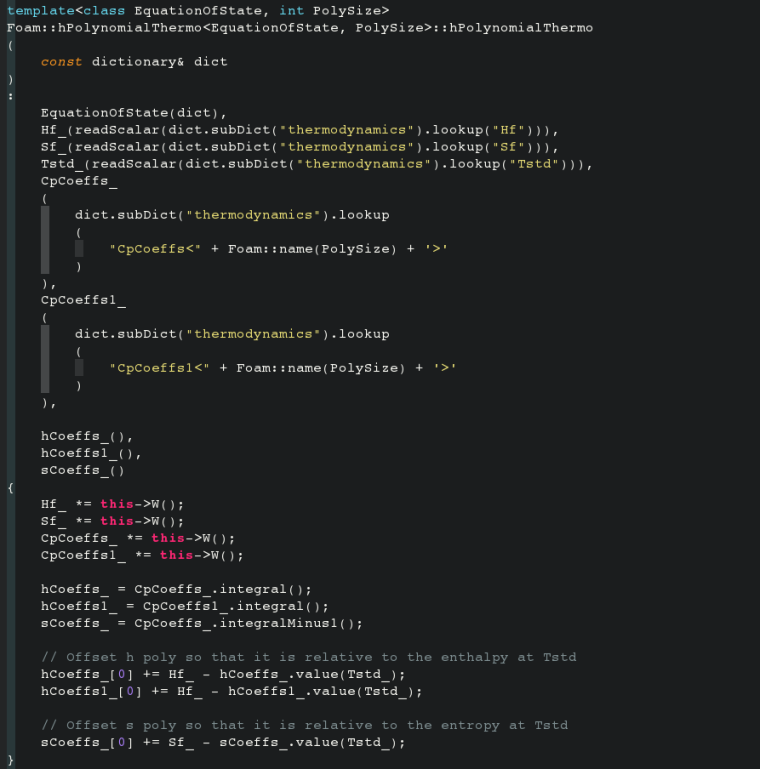
hPolynomialThermoI.H（这个是修改调用返回的焓值ha()）：
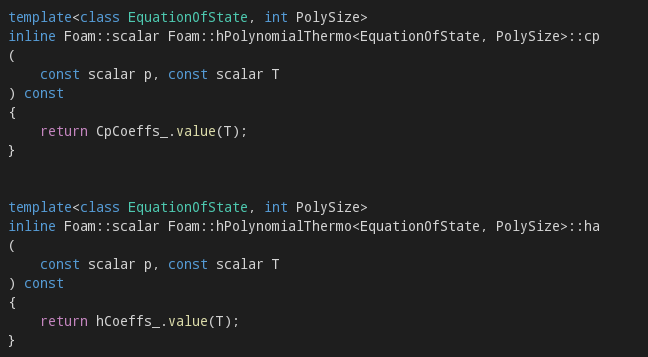
改动后：
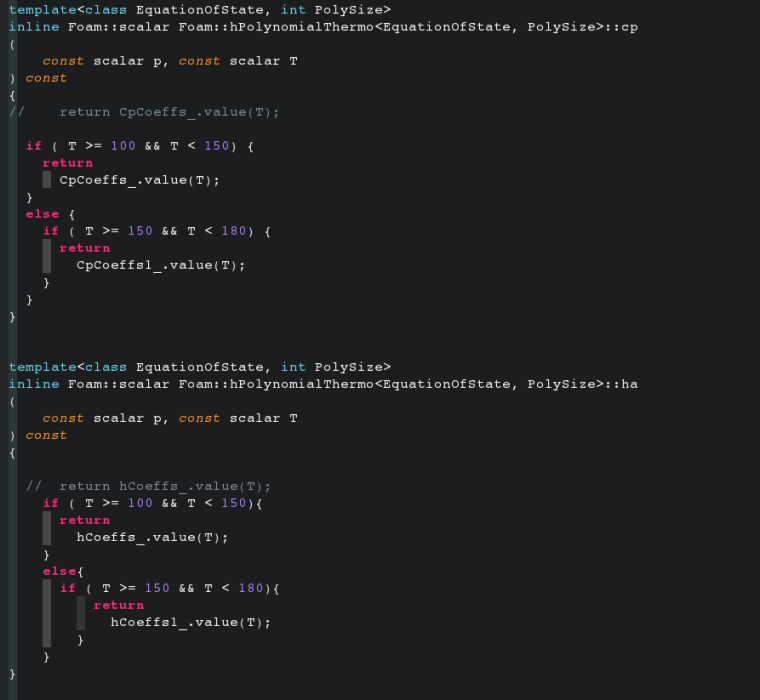
关于能量方程的求解过程的说明大家可以参考这篇文章：
一个具体能量方程的解析
我大概说一下hPolynomial热物理模型的一个基本思路：它是通过读取拟合的Cp(T)的多项式系数，然后通过Cp(T)的多项式系数求焓的多项式系数：CpCoeffs_ ( dict.subDict("thermodynamics").lookup ( "CpCoeffs<" + Foam::name(PolySize) + '>' ) ) CpCoeffs_ *= this->W(); hCoeffs_ = CpCoeffs_.integral(); // Offset h poly so that it is relative to the enthalpy at Tstd hCoeffs_[0] += Hf_ - hCoeffs_.value(Tstd_);最后通过ha()函数来返回焓值
ha(const scalar p, const scalar T) const { return hCoeffs_.value(T); }这个焓值与Cp的值一同返回然后去求温度T：
Cp：cp(const scalar p, const scalar T) const { return CpCoeffs_.value(T); }T的求解（文件在src/thermophysicalModels/specie/thermo/thermo/thermoI.H中的T()函数）：
Tnew = (this->*limit) (Test - ((this->*F)(p, Test) - f)/(this->*dFdT)(p, Test));
----这个引用的是上面提到的那篇文章。描述到此完毕。
-
好专业的问题。期待有人能给你回复。
你的模拟在 Temperature <180k 这个区间（蓝色曲线？），非常棒！180k以后，看到Cp的梯度明显增大，没有有试过更小的时间步长？更高阶的离散格式？
建议你直接联系那篇博客的作者，他或许能给你更直接的帮助。
-
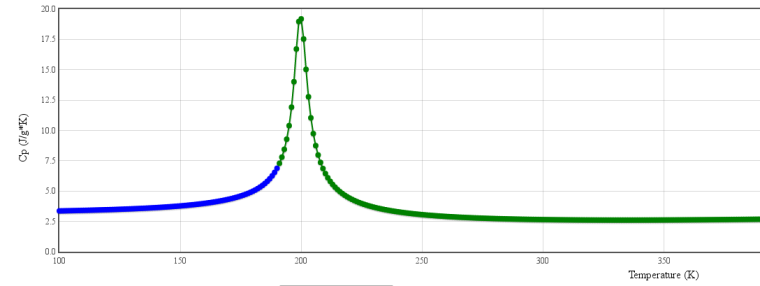
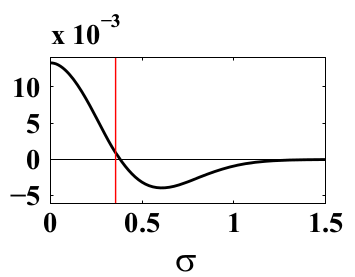
从这个图来看，Cp是一个存在极大值的曲线。如果楼主能确认T的函数也是存在极值的话。按照 @xpqiu 的解释，温度求解使用的为牛顿迭代法。牛顿迭代法如果某一解位于极值附近，必然发散不会收敛，则导致温度越界。你可以试试别的迭代法。
Test=-144277 Tnew=-288653 F=9.35162 f=-1.35014e+06 Cp=9.35162 Test=-288653 Tnew=-433029 F=9.35162 f=-1.35014e+06 Cp=9.35162 Test=-433029 Tnew=-577405 F=9.35162 f=-1.35014e+06 Cp=9.35162 Test=-577405 Tnew=-721781 F=9.35162 f=-1.35014e+06 Cp=9.35162 看起来这些温度越界了如果确认是这个问题的话，我建议采用Ridder求解。非常简单，并且对于下图这种存在极值的曲线也可以求解，或许OpenFOAM基金会也会对你这个工作感兴趣。
个人浅见，最好确定一下是不是我说的这个路子。
-
-
@random_ran 多谢。目前试验的拟合还在180K以内，所以还没涉及到Cp梯度大的情况。
-
我最初看错了范围，我以为你的曲线里包含了200K附近的那个间断点，所以才会说是牛顿法不适合。现在发现你的温度范围是100-180K，这一段就不包含间断点了，所以牛顿法应该没问题。
从你上面提供的调试信息，我认为主要问题在于，当T < 100K 和 T > 180K 时，你的cp函数将无定义，return 值是无定义的。你看出现开始发散的地方：Test=100.516 Tnew=99.569 F=-1.34695e+06 f=-1.35014e+06 Cp=3365.81 Test=99.569 Tnew=-144277 F=9.35162 f=-1.35014e+06 Cp=9.35162Tnew = 99.569 K ，小于100，此时，下一步得到的 Tnew就完全错了。我认为就是因为 99.569K对于的cp函数返回值无定义，程序不知道给你返回什么。
所以，我认为你程序里必须给出 T < 100 和 T > 180 时 cp 的定义。
另外，还有一个问题是，理论上如果能量值在正常范围内，应该牛顿法迭代得到的温度值不会小于100k，我相信你也是这么认为的。但是，据我的理解，那个迭代的函数里面，参数 f 对应的应该是能量（焓或者内能）。从你输出的信息来看，你的 f 的值似乎一直都是负数，这应该是不对的。所以，可能你的算例设置也有点问题。
以上仅供参考，欢迎讨论。
-
"Tnew = 99.569 K ，小于100，此时，下一步得到的 Tnew就完全错了。我认为就是因为 99.569K对于的cp函数返回值无定义，程序不知道给你返回什么。
所以，我认为你程序里必须给出 T < 100 和 T > 180 时 cp 的定义。"
——————————————————————————————
这个我有点疑问，我的初始值在130K或者更高，壁面加热在170K左右，算出来的温度怎么会低于100K，而且当我限定了cp 在 T < 100 和 T > 180 时 的情况，比如T < 100令T=100，T > 180 令T=180，结果用不了几步还是发散。“还有一个问题是，理论上如果能量值在正常范围内，应该牛顿法迭代得到的温度值不会小于100k，我相信你也是这么认为的。但是，据我的理解，那个迭代的函数里面，参数 f 对应的应该是能量（焓或者内能）。从你输出的信息来看，你的 f 的值似乎一直都是负数，这应该是不对的。”
———————————————————————————————
这个跟hPolynomial本身焓的设定有关系，他有一个参考值（偏移量）：hCoeffs_[0] += Hf_ - hCoeffs_.value(Tstd_);template<int PolySize> Foam::scalar Foam::Polynomial<PolySize>::value(const scalar x) const { scalar val = this->v_[0]; // avoid costly pow() in calculation scalar powX = 1; for (label i=1; i<PolySize; ++i) { powX *= x; val += this->v_[i]*powX; } if (logActive_) { val += logCoeff_*log(x); } return val; }理论上应该没问题，如果有问题那么在100～150K或150～180K也应当有问题。
-
有了点新发现，当在hPolynomialThermoI.H（src/thermophysicalModels/specie/thermo/hPolynomial/）的ha()函数中添加如下内容，能正常求解：
template<class EquationOfState, int PolySize> inline Foam::scalar Foam::hPolynomialThermo<EquationOfState, PolySize>::ha ( const scalar p, const scalar T ) const { if ( T >= 100 && T < 150){ return hCoeffs_.value(T); } else { return hCoeffs_.value(T); } }但是如果改为下面这种就求解不了（当然Cp也是跟着改的）：
template<class EquationOfState, int PolySize> inline Foam::scalar Foam::hPolynomialThermo<EquationOfState, PolySize>::ha ( const scalar p, const scalar T ) const { if ( T >= 100 && T < 150){ return hCoeffs_.value(T); } else { if ( T >= 150 && T < 180 ){ return hCoeffs1_.value(T);（实际上这里改为其他的比如多项式，查表之类的都一样） } else { return hCoeffs_.value(T); } } }template<class EquationOfState, int PolySize> inline Foam::scalar Foam::hPolynomialThermo<EquationOfState, PolySize>::cp ( const scalar p, const scalar T ) const { // return CpCoeffs_.value(T); if ( T >= 100 && T < 150){ return CpCoeffs_.value(T); } else { if ( T >= 150 && T < 180 ){ return CpCoeffs1_.value(T); } else { return CpCoeffs_.value(T); } } }感觉问题是由这里引起的。
-
@李东岳 @xpqiu
我想我可能找到原因了：因为单段拟合时，Cp系数组成的多项式计算的Cp连续（Cp连续），进而由Cp系数算出的焓he的系数组成的多项式算出的焓he连续（焓值连续）。而当多段拟合时，由于各段Cp系数不一致导致算出的焓值he与其它多项式的焓值不连续，导致出现焓值跳跃点（焓值间断）。在焓值间断点算出的（h1-h0）异常而导致温度异常，最终发散。
对于这种情况是否还有其他出路？求教！:crying:CpCoeffs1_ *= this->W(); hCoeffs_ = CpCoeffs_.integral(); hCoeffs_[0] += Hf_ - hCoeffs_.value(Tstd_); return hCoeffs_.value(T);template<int PolySize> Foam::scalar Foam::Polynomial<PolySize>::value(const scalar x) const { scalar val = this->v_[0]; // avoid costly pow() in calculation scalar powX = 1; for (label i=1; i<PolySize; ++i) { powX *= x; val += this->v_[i]*powX; } if (logActive_) { val += logCoeff_*log(x); } return val; }template<int PolySize> typename Foam::Polynomial<PolySize>::intPolyType Foam::Polynomial<PolySize>::integral(const scalar intConstant) const { intPolyType newCoeffs; newCoeffs[0] = intConstant; forAll(*this, i) { newCoeffs[i+1] = this->v_[i]/(i + 1); } return newCoeffs; } -
@深白色
h间断，newton法可能会来回迭代。还有，你那个临界点附近的cp曲线看着像Runge函数，这玩意儿用多项式拟合本来就不合适，参考
-
@程迪 多谢指教。焓值不连续可以通过光顺进行处理。这个问题本身研究的就是分多段多项式来解决Runge现象。
-
@深白色 您好，打扰您了，请问highcpcoeffs、lowcpcoeffs具体的取值是怎么取的呢？对此非常困惑，不知道这里面的七个系数是从哪里得来的？
-
老师们好，关于janaf我发现教程里的算例中对于同一气体它的a1到a7的值取得不一样（hotBoxes和simplifiedSiwek），如果都是查表得出的数据的话那为什么不一样，是因为不同的压力温度下需要查不同的表吗？还是表一直在不断更新？希望老师们能指点迷津，非常感谢！
