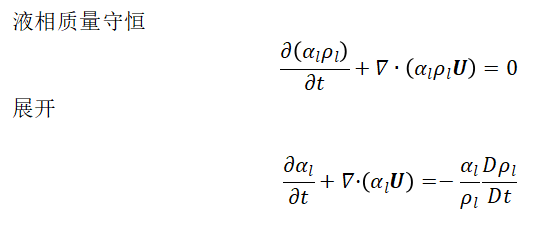关于VOF模型中相体积分数方程的疑问。
-
@Tens 在 关于VOF模型中相体积分数方程的疑问。 中说:
I encourage the authors to add all turbulent contributions: for the liquid volume fraction, as it is a scalar, it is possible to add an eddy-diffusivity model to the volume fraction equation(which will certainly remove any need for an artificial compression model required in DNS)
We agree with the reiviewer that the turbulent contribution should be added in the phase fraction transported equation. In our work, RANS model was used and the phase fraction equation can be written as the following:
$$
\frac{\p \overline{\alpha+\alpha'}}{\p t}+\nabla\cdot(\overline{\bfU}\overline{\alpha+\alpha'}) =0
$$
where $\alpha'$ is a fluctuating component for the phase fraction and the second term of the equation can be calculated by Reynolds decomposition:
$$
\overline{\bfU}\overline{\alpha+\alpha'}=\overline{\bfU}\overline{\alpha}+\overline{\bfU}\alpha'
$$
in which the $\overline{\bfU}\alpha'$ is the so-called turbulent flux of the phase fraction. When a gradient-diffusion model is enplyed, it can be written as
$$
\overline{\bfU}\alpha'=-D_{\alpha}\nabla \overline{\alpha}
$$
where $D_{\alpha}$ is the modelled diffusion. In this way, the phase fraction can be written as
$$
\frac{\p \overline{\alpha+\alpha'}}{\p t}+\nabla\cdot(\overline{\bfU}\overline{\alpha}) -\nabla\cdot(D_{\alpha}\nabla \overline{\alpha})=0
$$
and the thrid term is the turbulent contribution as said by the reviewer. The turbulent contribution was proven to be important for slurry flow simulations [1,2,3,4]. However, in our work it was used to simulate gas-liquid flow and its contribution was typically neglected [5,6,7].- Numerical prediction of fully-suspended slurry flow in horizontal pipes
- Improvements in the numerical prediction of fully-suspended slurry flow
- Analysis and discussion of two fluid modelling of pipe flow of fully suspended slurry
- A general two-phase turbulent flow model applied to the study of sediment
- Computational Models for Turbulent Reacting Flows
- Computational Models for Polydisperse Particulate and Multiphase Systems