多孔介质多组分,交界面处真实物理场不连续
-
FLUENT 中计算组分输运的公式为
\begin{equation}
\frac{\partial{\rho Y_i}}{\partial t} +\nabla\cdot(\rho \vec{v} Y_i)=\nabla \cdot (\rho D_i\nabla Y_i)) +S_i
\end{equation}如果有三个连续的计算区域(区域之间边界条件为interior), 有两个区域为孔隙度不同的多孔介质.
我同时打开多孔介质模型和组分输运模型.
计算的组分浓度场($c_i$)是表象浓度场(superficial)吗?
如果表象浓度场在交界面处是连续的, 那么将表象浓度场($c_i$)除以孔隙度得到的真实浓度场在交界面处就是不连续的, 这似乎不太合理.
请问有人遇到过类似问题吗? -
@kdfluxit
不好意思, 问题编辑的不合适, 重新编辑一下问题
FLUENT 中计算组分输运的公式为\begin{equation}
\frac{\partial{\rho Y_i}}{\partial t} +\nabla\cdot(\rho \vec{v} Y_i)=\nabla \cdot (\rho D_i\nabla Y_i)) +S_i
\end{equation}如果有三个连续的计算区域(区域之间边界条件为interior), 有两个区域为孔隙度不同的多孔介质.
如图所示
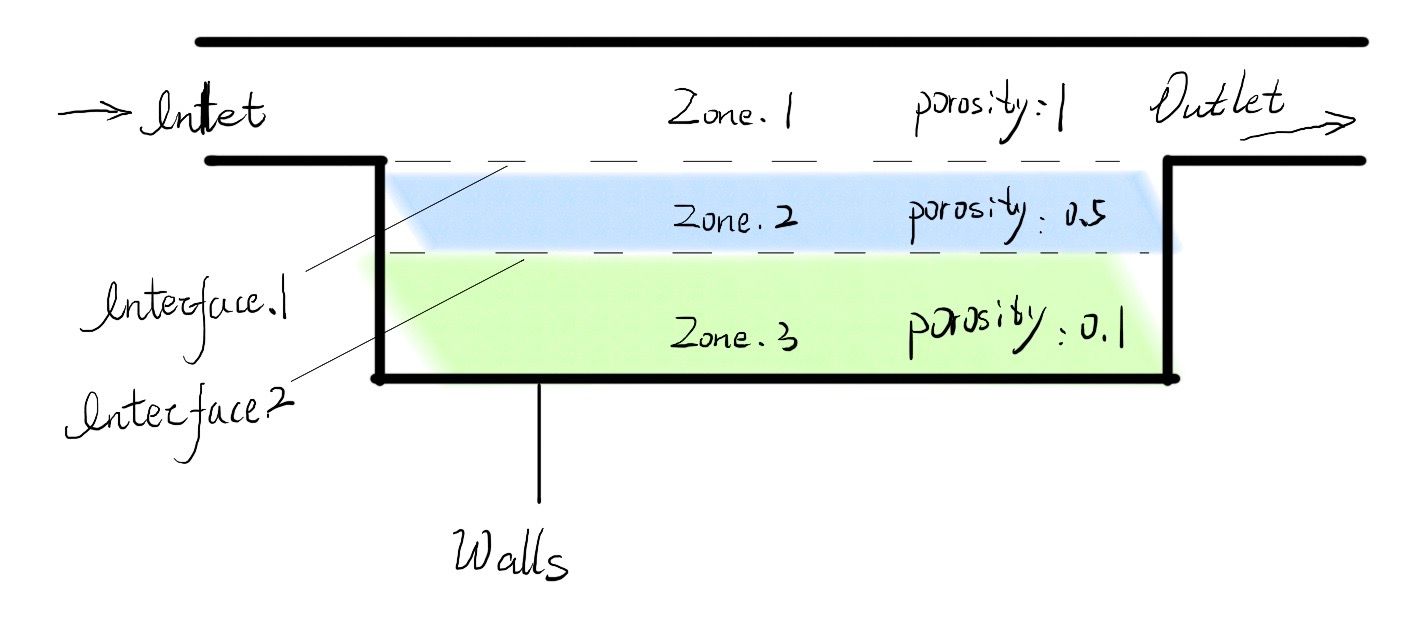
Zone.1为非多孔介质;
Zone.2为孔隙度($\epsilon_2$)为0.5的多孔介质;
Zone.3为孔隙度($\epsilon_3$)为0.1的多孔介质;有两个关注的交界面, Interface.1(Zone.1和Zone.2)和Interface.2(Zone.2和Zone.3)
我同时打开多孔介质模型和组分输运模型.
请问
1.计算的组分浓度场($c_i$)是表象浓度场(superficial)吗?
2.如果表象浓度场在交界面处是连续的, 那么两个区域在交界面处, 将表象浓度场($c_i$)除以孔隙度($\epsilon_2$和$\epsilon_3$)得到的真实浓度场在交界面处就是不连续的, 这似乎不太合理.
请问有人遇到过类似问题吗? -
@东岳
谢谢您的关注;
**表象物理量:**以组分摩尔浓度为例 在多孔介质中, 如果有一个控制体的体积是$V$, 控制体中孔隙的体积是$V_{pore}$, 这个控制体中某个的摩尔数为$n$, 表象浓度(superficial)为$\frac{n}{V}$, 这个浓度在将固体不分考虑进入了体积, 因此不是真实物理的浓度, 孔中的浓度为$\frac{n}{V_{pore}}$;
由于上述方程中的$\rho$,是表象的量(质量除以控制体体积$V$), 因此在交界面处, 也是表象$\rho$连续. 因为求解的是连续方程, 交界面两侧的$\rho$是连续的, 但是将交界面两侧的表象量$\rho$换算成物理量, 就应该用表象量除以孔隙度, 即:
$\frac{\rho}{\epsilon_{zone.1}}$,$\frac{\rho}{\epsilon_{zone.2}}$.
这就会导致, 在交界面处, 表象的量$\rho$连续, 但是真实物理量$\frac{\rho}{\epsilon}$不连续
回复: 多孔介质多组分
谢谢您的关注;
表象物理量以组分质量浓度ρ为例 在多孔介质中, 如果有一个控制体的体积是V, 控制体中孔隙的体积是Vpore, 这个控制体中某个组分的质量为m, 表象浓度(superficial)为ρ=mV, 这个浓度在将固体部分考虑进入了体积, 因此不是真实物理的浓度, 孔中的浓度为$\rho p=\frac{m}{V{pore}}$;由于上述方程中的\rho是表象的量(质量m除以控制体体积V),因此在交界面处,也是表象质量浓度连续.因为求解的是连续方程,交界面两侧的是连续的,但是将交界面两侧的表象量$\rho=\frac{m}{V}$换算成物理量$\rho_p=\frac{m}{V}$,就应该用表象量除以孔隙度,即:$\rho_p=\frac{\rho}{\epsilon}$,$\epsilon = \frac{V_{pore}}{V}$这就会导致,在交界面处,表象的量$\rho$连续,但是真实物理量$\rho _{pore}$不连续 -
其实真正严格研究这个问题 目前还不可解 你采用fluent可以不用管这些 因为fluent 如果你选的默认superficial选项 求解多孔介质的时候 不考虑孔隙率 只有在非稳态项才考虑 那么实际流场跟孔隙率就无关 然后切向的速度用适当的该方向的阻力系数来模化 一般可以近似成为无滑移的条件 因为你用fluent那么还是精度和稳定的折中了 这种办法是最佳收敛手段 表观速度这个词最早是针对颗粒层床的经验数据 就是流量除以过滤面积 也是不考虑孔隙率的
关于这方面真做研究目前存在介面连续和不连续两种模型 但是我试过几乎都难收敛 实际上真实情况介面浓度更接近不连续 你如果有兴趣真的做深这部分我给你提供参考 但是我个人建议不要深入搞这块 严格来说 fluent除开压降 其他的都是错的 但是他能算整体设备 其他方式复杂几何目前都不能收敛flowporous.doc -
@l-j刘侃
谢谢你的关注. 感谢你的资料, 我会认真了解一下.我目前关注的燃料电池的气体扩散层, 其厚度大概在200微米左右, 一般入口气体的速度与气体扩散层表面平行;
但是仍然有一定的对流; 而且在这个很薄的区域内, 很可能这些对流对物质的输运比扩散更强. 对于目前的研究而言, 即使是 $10^-3$ m/s这个量级的速度都是值得注意的.
因此, 我比较关注速度的计算, 尤其是气流从通道进入气体扩散层那个界面的速度.另外
, 我参看过ANSYS FLUENT 18.2手册中 7.1.1.Species Transport Equations, 这里面说到, 如果计算瞬态, 就在瞬态的项上乘以一个孔隙度 $\epsilon$ , 方程就变成了
$\frac{\partial \epsilon \rho Y_i}{\partial}$=
右边的项与没有孔隙度时没有区别. 我项问一下, 我这样理解对吗?另外2
同样在手册中 6.2.3.8. Modeling Porous Media Based on Physical Velocity
里面谈到, 如果开启物理速度后标量方程的计算就是$\frac{\partial }{\partial t}(\epsilon \rho \phi) + \nabla \cdot (\epsilon \rho \vec{v} \phi) = \nabla \cdot (\epsilon \rho \Gamma \nabla \phi) + \epsilon S_{\phi}$
这样看起来计算的就是物理速度了. 是否会对计算的准确性有一定帮助呢?
---- 这里我想请教一下, 虽然FLUENT计算的结果不对, 但是受压力驱动进入气体扩散层的趋势是否合理呢?
或者FLUENT的这种计算方案, 哪些变量的趋势是比较合理的? -
物理速度和这不相关 物理速度描述多孔的统计了孔隙率的速度 但是实际上除非你是固定孔道的多孔板式 才能够很好的预计内部速度 与理论计算速度可能比较符合 因为中间真实速度也不好测量 我在某吊桥线缆上有过项目实测经验这种方式预测得还不错 而关于浓度连续性 你的设想是在一个连续的流道内他的浓度是连续变化的 那么这个连续流道实际上已经属于需要对多孔介质直接建立模型 这种方式你可以具备连续性 但是fluent处理是经验公式性的 不是真正求解通道的 所以实际上你的浓度当在一个cell zone求解时 当进入下一个多孔介质孔隙率跳跃变化的cell zone时 他直接会利用这个cell zone的porosity求解来得出这个cell zone cell内部的值 它不需要保证连续性 实际上fluent不太可能实现预测准确分布 但是如果你的结构很大并且分布比较均匀的时候 fluent能够大概预测一下趋势
