关于动量方程表面源项的离散问题
-
是可以相乘,所以最后的问题是,一些书里面写$\int \nabla\cdot\bfU\rd V=\int_s\bfU\cdot\mathbf{n}\rd S$,一些书里面写$\int \nabla\cdot\bfU\rd V=\int_s\mathbf{n}\cdot\bfU\rd S$ ,然后两个还不相等?
就像一些书里面写速度的散度是
\begin{equation}
\label{gradientV}
\nabla \mathbf{U} = \left[
\begin{matrix}
\frac{\partial u_1}{\partial x} & \frac{\partial u_2}{\partial x} & \frac{\partial u_3}{\partial x}\\
\frac{\partial u_1}{\partial y} & \frac{\partial u_2}{\partial y} & \frac{\partial u_3}{\partial y} \\
\frac{\partial u_1}{\partial z} & \frac{\partial u_2}{\partial z} & \frac{\partial u_3}{\partial z}\\
\end{matrix}
\right]
\end{equation}
一些书里面写成了
\begin{equation}
\nabla \mathbf{U} = \left[
\begin{matrix}
\frac{\partial u_1}{\partial x} & \frac{\partial u_1}{\partial y} & \frac{\partial u_1}{\partial z}\\
\frac{\partial u_2}{\partial x} & \frac{\partial u_2}{\partial y} & \frac{\partial u_2}{\partial z} \\
\frac{\partial u_3}{\partial x} & \frac{\partial u_3}{\partial y} & \frac{\partial u_3}{\partial z}\\
\end{matrix}
\right]
\end{equation}
对于后一个问题,之前找过资料是CFD里面要写成第一种形式。对于高斯定律那个问题,我更喜欢这么写 $\int \nabla\cdot\bfU\rd V=\int_s\bfU\cdot\mathbf{n}\rd S$,开起来更通顺:速度乘以面试量=通量。谁有更确定的信息也可以恭喜下
-
@Mrc-Young @东岳
两个矢量点乘是标量,左右点乘都相等。
问题是不知道有没有矢量左点乘张量,若有的话,其与张量右点乘矢量的结果是不是相等。有:
Nabla算子左点乘二阶张量A=二阶张量A的转秩右点乘Nabla算子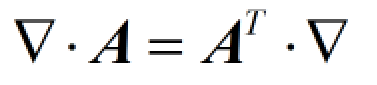
但如果把上面的Nabla算子换成矢量,上式还成立么??

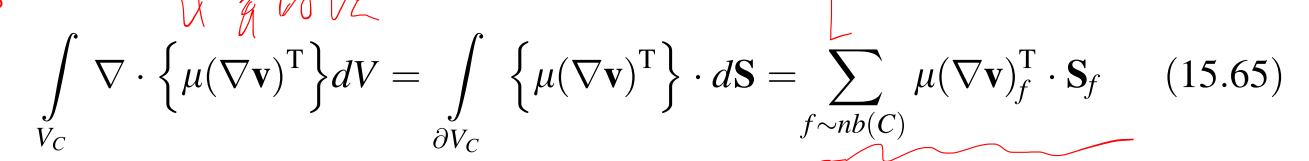
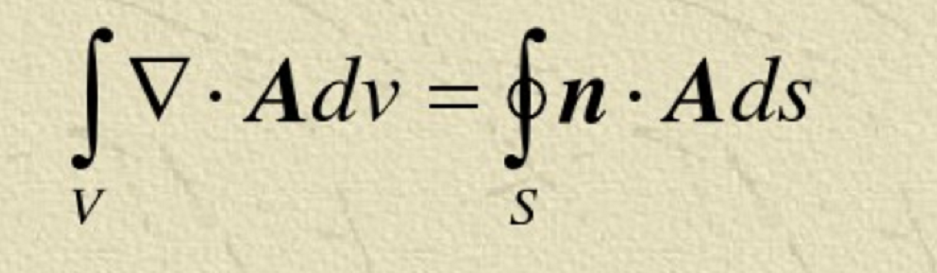
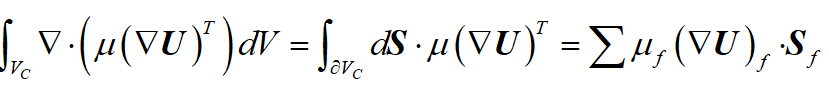
 看起来nA乘不了
看起来nA乘不了
 )
)