关于群体平衡方程中sectional method (Gelbard & Seinfeld)的守恒性
-
sectional method 最早由Caltech 的Seinfeld提出,意即把连续的颗粒大小(如直径,体积等)分成数个section,在每个section内假定颗粒均匀分布(也可其他分布),然后求解离散方程。
1996年Ramkrishna等人提出了fixed pivot method,本质上对Seinfeld 的 Sectional Method 进一步简化,认为在每个section内颗粒分布于某一个粒径或体积上(representative size or pivot)。因为任意两个pivots的颗粒相互凝聚,所产生的新颗粒未必仍落在pivot上,所以新颗粒需要根据某两个矩来分配。
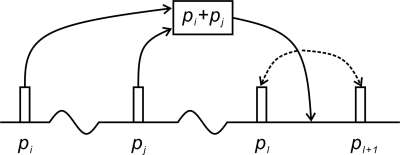
但是,问题在于这些守恒问题并不会在sectional method中遇到,因为sectional method 假定在某个section内均匀分配,而非集中于某些representative size上。
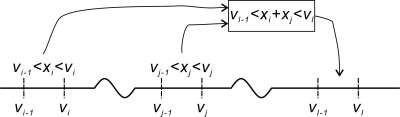
所以,我认为sectional method并非如Ramkrishna断言,只能守恒一个矩。 -
@东岳
Ramkrishna的fixed pivot method可以保证两个矩守恒,而Seinfeld的方法只能守恒一个矩,但是可以通过不同的方程守恒任意一个。我大概明白了。
Gelbard和Seinfeld的文章链接,我不知道怎么传PDF
https://www.sciencedirect.com/science/article/pii/002197978090394X
另外,Gelbard和Seinfeld的方法可以通过解多个方程组得到多个守恒矩,比如n(m0),s(m2/3),v(m1),v^2(m2)。这算是一个优势么? -
moment method对于nucleation和condensation的模拟简单吗?
即为简单。但是溶解/蒸发数值上要复杂些。2017年我在HZDR的时候同事用fixed pivot method模拟增长,我用moment method,相比来看moment method要更简单,并且不需要处理相空间的drift:https://www.sciencedirect.com/science/article/pii/S1004954118301174/pdfft?md5=84216a8842ce3fd6d1a99d4f327c1ee1&pid=1-s2.0-S1004954118301174-main.pdf
