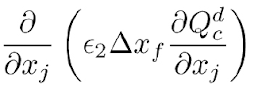Artificial dissipation 项
-
大家好，
我想在一个动量方程中加入一项Artificial dissipation term，如下所示：
其中epsilon2 is the second order dissipation coefficient.
但是我没有找到关于这项更详细的介绍，比如如何对这个系数取值。
请问有没有前辈可以指点一下，哪里可以找到相关的资料？谢谢大家！
-
epsilon2 is the second order dissipation coefficient
还不知道专业教材里面这个叫什么
-
@李东岳 我的droplet phase的convective flux只有rhoUU, 右边只有一个drag force，所以很不稳定。并且我使用runge-kutta递进，explicit更不稳定。。。现在想植入AUSM scheme，但是简单看了一下发现虽然AUSM有气液两相的，但是是把液相看成是contunumm的，而我的液相是dispersed. 是在气相里的droplet。。
不知道东岳师兄有没有什么建议~ -
我的droplet phase的convective flux只有rhoUU, 右边只有一个drag force，所以很不稳定。但是是把液相看成是contunumm的，而我的液相是dispersed. 是在气相里的droplet。。
从描述来看你在研究时间高阶格式？但是是基于双流体模型么？双流体默认都是连续的。
Openfoam自带的双流体模型有改动么。你的动量方程是什么？
-
@李东岳 我的模型是先计算空气流场，再算流场中的液滴。
关于液滴运动的Euler动量方程是：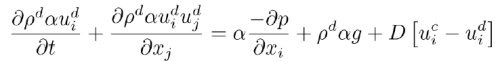
时间项用4 stage Runge-kutta 来递进，这里虽然加入了压力梯度但是还是不稳定。
我的第一个问题是：如何close这里的压力？我看到有些人在直接用空气场的压力，还有的是用stiffened-gas equation of state来解压力。
第二个问题是：如何给droplet field的动量方程加入一些dissipation, 使得计算更加稳定。因为我在做transonic，所以shock的形成导致计算很不稳定。。。之前打算植入AUSM scheme，但是看到目前的paper做的都是两相分离的那种，不是我这种混合在一起的。。对多项并没有什么经验。。感谢指导！
-
先确认一下：你这个方程不就是动量方程么？整合在一起不就是双流体模型么？然后不就是双流体模型+龙哥库塔时间步进么？
-
@李东岳 嗯这个方程式动量方程。是two phase flow
-
如何close这里的压力？我看到有些人在直接用空气场的压力，还有的是用stiffened-gas equation of state来解压力
双流体模型压力是平均压力。是用simple或者piso求解的。你看的文献有地址么，发来看看
-
@李东岳 比如这一篇：’Numerical prediction of airfoil characteristics in a transonic droplet-laden air flow‘， Geum-Su Yeom ⇑, Keun-Shik Chang, Seung Wook Baek. 他们用了stiffened gas equation of state. 我之前已经在rhoPimpleFoam 中植入了液态的控制方程，算的结果也得到了验证，但无奈老板让做density based solver，所以不能用piso来解。。
-
如何close这里的压力？我看到有些人在直接用空气场的压力，还有的是用stiffened-gas equation of state来解压力
这篇文章求解的也是双流体模型，但是求解策略非传统方法，即采用Operator Split的方式求解，也就是
3. Numerical Methods中所说的fractional-step。不同领域的叫法不同，但思想相同。这种方法（暂且称之为新方法）求解的也是动量方程。 和传统方法的区别在于：- 传统方法直接求解动量方程
- 新方法第一步只考虑对流扩散（方程17），然后考虑源项ODE（方程18），类似拉格朗日
新方法中压力通过方程2计算而来。
