计算y+,Δx+,Δz+的疑问
-
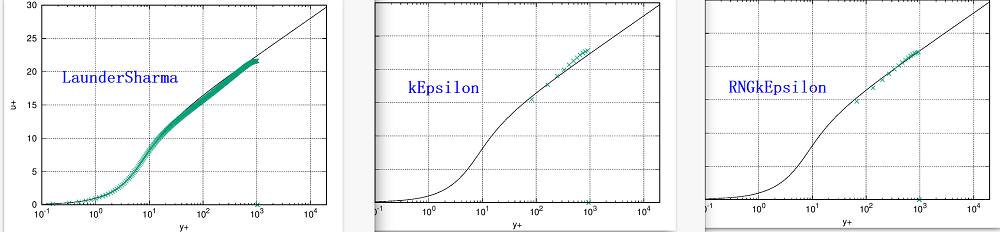
最近看到一个文章:CFD计算中,除了y+,还应知道Δx+,Δz+【学习笔记】,但关于计算这几个参数有几点疑问:
- 根据yPlus在openfoam代码里面的实现,以及公式$y^{+}=\frac{U_{\tau}y}{\nu }$,由于同个垂直位置处用的$U_{\tau}$都是一样的,那么计算流场垂直于壁面其他高度
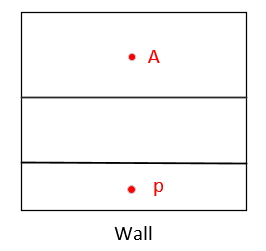
A位置的$y^{+}$,是否可以先用后处理程序yplus得到第一层边界层网格p的$y^{+}$,然后直接通过A与p的高度的比值求得A位置的$y^{+}$?
$y_{A}^{+}=y_{p}^{+}\times \frac{y_{A}}{y_{p}}$
2.类似第1个问题,计算第一层网格的$\bigtriangleup x^{+}$和$\bigtriangleup z^{+}$,用的$U_{\tau}$都是一样的,也类似可以通过长度比值求得?
$\bigtriangleup x^{+}=\frac{U_{\tau}\bigtriangleup x}{\nu }=y^{+}\times \frac{\bigtriangleup x}{y}$
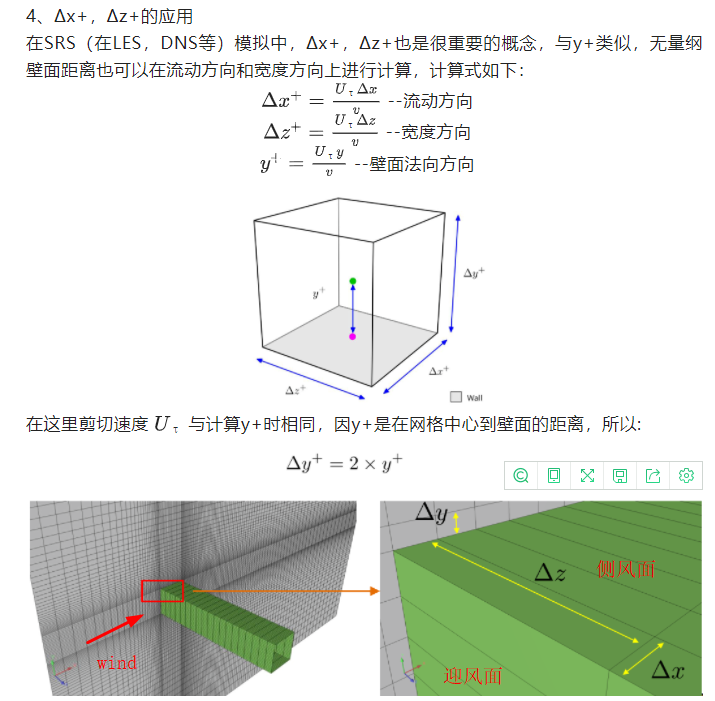
$\bigtriangleup z^{+}=\frac{U_{\tau}\bigtriangleup x}{\nu }=y^{+}\times \frac{\bigtriangleup z}{y}$3.$\bigtriangleup x^{+}$和$\bigtriangleup z^{+}$的方向定义问题。假设风向如图所示,对于侧风面流动方向和宽度方向比较好理解。但对于迎风面,风方向就直接是壁面法向方向,此时的$\bigtriangleup x^{+}$和$\bigtriangleup z^{+}$的方向该如何定义?
4.根据文献《Piomelli, U. and J.R. Chasnov, Large-eddy simulations: theory and applications, in Turbulence and transition modelling. 1996, Springer. p. 269-336.》,对于wall-resolved LES,要求$\bigtriangleup x^{+}\simeq 50\sim 150$,$\bigtriangleup z^{+}\simeq 15\sim 40$,对这两个方向的要求区别还挺大,对应第3个问题这两个方向具体在模型中不同面如何定义,可能会得到不一样的结果。

5.最后的问题是LES计算满足了$y^{+}$,但$\bigtriangleup x^{+}$和$\bigtriangleup z^{+}$比值超过了文献建议范围,对结果影响会很大吗?
最后感谢各位大佬帮忙解惑
- 根据yPlus在openfoam代码里面的实现,以及公式$y^{+}=\frac{U_{\tau}y}{\nu }$,由于同个垂直位置处用的$U_{\tau}$都是一样的,那么计算流场垂直于壁面其他高度
-
- 首先计算 $\bigtriangleup x^{+}$、$\bigtriangleup z^{+}$,是根据下面的公式由$\ y^{+}$推算得到
1.根据yPlus在openfoam代码里面的实现,以及公式$y^{+}=\frac{U_{\tau}y}{\nu }$,由于同个垂直位置处用的$U_{\tau}$都是一样的,那么计算流场垂直于壁面其他高度A位置的y+,是否可以先用后处理程序yplus得到第一层边界层网格p的y+,然后直接通过A与p的高度的比值求得A位置的y+?
$y_{A}^{+}=y_{p}^{+}\times \frac{y_{A}}{y_{p}}$2.类似第1个问题,计算第一层网格的△x+和△z+,用的Uτ都是一样的,也类似可以通过长度比值求得?
$\bigtriangleup x^{+}=\frac{U_{\tau}\bigtriangleup x}{\nu }=y^{+}\times \frac{\bigtriangleup x}{y}$
$\bigtriangleup z^{+}=\frac{U_{\tau}\bigtriangleup x}{\nu }=y^{+}\times \frac{\bigtriangleup z}{y}$2.模拟的结论可参考文献《Chen, L., et al., Consistency improved random flow generation method for large eddy simulation of atmospheric boundary layer. Journal of Wind Engineering and Industrial Aerodynamics, 2022. 229: p. 105147.》,模拟对象是高层建筑,对于建筑表面的△x+、△z+、y+近似符合要求,风压模拟结果跟实验值吻合较好。但计算域底面虽然不符合要求,但从结果看对高层建筑影响较小。

-
@李东岳 李老师,看这篇文章《Komen, E., et al., A quantification method for numerical dissipation in quasi-DNS and under-resolved DNS, and effects of numerical dissipation in quasi-DNS and under-resolved DNS of turbulent channel flows. Journal of computational physics, 2017. 345: p. 565-595.》有提到WRLES中$\Delta x^+$,$\Delta z^+$要求:

-
@李东岳 李老师,现在理解了其他位置的$y^+$可以通过壁面第一层网格的$y^+_{st}$的高度比例求得,但主要的一个困惑点是如何判断方向的问题。对于槽道流,这个方向没有争议;但如果放了建筑后,比如下面描述的迎风面,流动方向与壁面方向重合,其他两个方向似乎都是宽度方向,此时$\Delta x^+$和$\Delta z^+$就不好判断。
我的做法是因为网格是近似于边长相等的多面体网格,那么就不用区分$\Delta x^+$和$\Delta z^+$,因为其值结果是近似一样的。但有的文献又对$\Delta x^+$和$\Delta z^+$提出的要求范围没有交集,只能大概的设定在两个没有交集范围的中间位置。3.$\bigtriangleup x^{+}$和$\bigtriangleup z^{+}$的方向定义问题。假设风向如图所示,对于侧风面流动方向和宽度方向比较好理解。但对于迎风面,风方向就直接是壁面法向方向,此时的$\bigtriangleup x^{+}$和$\bigtriangleup z^{+}$的方向该如何定义?

-
@李东岳
李老师,看了OpenFOAM中yPlus计算,是通过壁面网格最近垂直距离算的,也就是y+算的是壁面垂直方向,这个方向没有争议。有争议的是网格不是槽道流那种网格,网格面与流动方向有一定夹角,那么其他两个方向,如何判定是$\Delta x^+$还是$\Delta z^+$
OpenFOAM中
yPlus计算方法:Foam::tmp<Foam::volScalarField> Foam::functionObjects::yPlus::calcYPlus ( const momentumTransportModel& turbModel ) { tmp<volScalarField> tyPlus ( volScalarField::New ( IOobject::groupName(type(), phaseName_), mesh_, dimensionedScalar(dimless, 0) ) ); volScalarField::Boundary& yPlusBf = tyPlus.ref().boundaryFieldRef(); volScalarField::Boundary d = nearWallDist(mesh_).y(); const volScalarField::Boundary nutBf = turbModel.nut()().boundaryField(); const volScalarField::Boundary nuEffBf = turbModel.nuEff()().boundaryField(); const volScalarField::Boundary nuBf = turbModel.nu()().boundaryField(); const fvPatchList& patches = mesh_.boundary(); forAll(patches, patchi) { const fvPatch& patch = patches[patchi]; if (isA<nutWallFunctionFvPatchScalarField>(nutBf[patchi])) { const nutWallFunctionFvPatchScalarField& nutPf = dynamic_cast<const nutWallFunctionFvPatchScalarField&> ( nutBf[patchi] ); yPlusBf[patchi] = nutPf.yPlus(); } else if (isA<wallFvPatch>(patch)) { yPlusBf[patchi] = d[patchi] *sqrt ( nuEffBf[patchi] *mag(turbModel.U().boundaryField()[patchi].snGrad()) )/nuBf[patchi]; } } return tyPlus; } -
@李东岳 李老师,植入思路我想可以根据与y+的关系来实现,但最后还是回归到网格除了法向外,另外两个方向怎么定义x和z方向。其实在网格与风向有夹角时候,已经无法严格区分顺流向和宽度方向了
2.类似第1个问题,计算第一层网格的$\bigtriangleup x^{+}$和$\bigtriangleup z^{+}$,用的$U_{\tau}$都是一样的,也类似可以通过长度比值求得?
$\bigtriangleup x^{+}=\frac{U_{\tau}\bigtriangleup x}{\nu }=y^{+}\times \frac{\bigtriangleup x}{y}$
$\bigtriangleup z^{+}=\frac{U_{\tau}\bigtriangleup x}{\nu }=y^{+}\times \frac{\bigtriangleup z}{y}$