q-DNS计算槽道流遇到了一些问题，求大神们指点

悬铃神木

我想用q-DNS模拟一个Re_tau=180的槽道湍流,网格与这篇链接文本文献中基本相同。

0_1546246841602_网格.PNG

我更改了一下icoFoam的计算公式，代码包：0_1546247060398_pGradIcoFoam.zip

具体改法如下：

createFields.H中，添加一个pGrad场，量纲与压力梯度相同，大小直接给出：

volVectorField pGrad
(
    IOobject
    (
        "pGrad",
        runTime.timeName(),
        mesh,
        IOobject::NO_READ,
              //MUST_READ,
        IOobject::AUTO_WRITE
    ),
    mesh,
    dimensionedVector("pGrad",dimensionSet(0, 1, -2, 0, 0),vector(-1,0,0))
);

动量预测方程中把pGrad项加入到方程右边，与压力梯度项并列

        {
            solve(UEqn == -fvc::grad(p）-pGrad);
        }

压力泊松方程中也加入pGrad项带来的影响

         fvScalarMatrix pEqn
         (
             fvm::laplacian(rAU, p) + fvc::div(rAU\*pGrad) == fvc::div(phiHbyA)
         );

还有最后一步的速度修正：

U = HbyA - rAU\*fvc::grad（p）- rAU\*pGrad;

另外，还有按照苏老师博客里的方法，把icoFoam改为可以变时间步长的求解器
加入计算并输出平均速度的代码：

        scalar magUbarAve = 0.0;
        scalar V = 0.0;
        const scalarField& cv = mesh.V();
        vector flowDir_ = vector(1,0,0);
        for(label celli=0; celli < mesh.C().size() ; celli++)
        {
            scalar volCell = cv[celli];
            V += volCell;
            magUbarAve += (flowDir_ & U[celli])*volCell;
        }

        reduce(magUbarAve, sumOp<scalar>());
        reduce(V, sumOp<scalar>());

        magUbarAve /= V;
        Info << "Ubar = " << magUbarAve  << endl;

计算算例：

0_1546249122420_channel180.zip

计算初始场用perturbU工具进行打乱，然后计算一些时间步获得完全发展的湍流场

我现在遇到的问题是，计算一段时间后，发现靠近边界层的速度算得还比较准，但是槽道中部远离边界层的地方出现奇怪的脉动

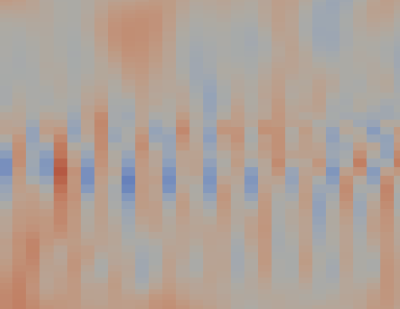
放大可看到这个脉动大概以三个cells为一个周期。
最奇怪的是平均速度型竟然上下不对称

已做时间足够长的平均

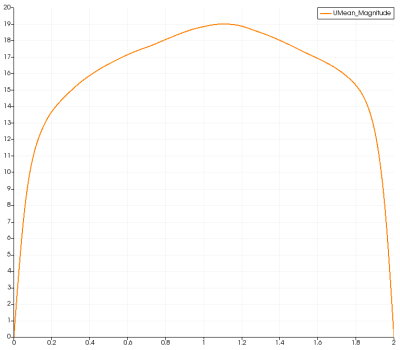
我的改动中应该没有会引起这种不对称的地方？

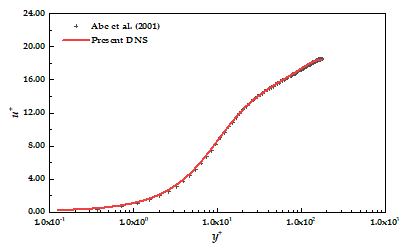
壁面律图像和雷诺应力图像也同样，壁面处算得还好，中间算不好

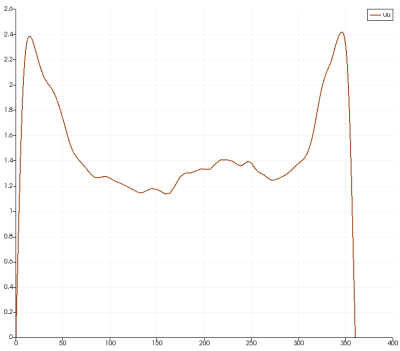
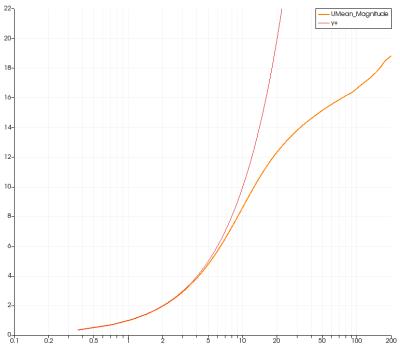
似乎可能是中间网格不够密的原因？但是我使用的网格应该和那篇参考文献中相同啊，他也用的是openFoam做的q-DNS，但他得到的结果就很好，所以我现在不知道错在什么地方。
我修改后的求解器、算例的基本设定都已上传，希望各位老师能帮忙指点一下，不胜感激！

李东岳

你的平均速度代码看起来不正确。

不过现在你不需要做求解器了，你尝试用pisoFoam层流求解，然后再fvOptions中添加

momentumSource
{
    type            meanVelocityForce;
    active          yes;
 
    meanVelocityForceCoeffs
    {
        selectionMode   all;
 
        fields          (U);
        Ubar            (0.1 0 0);//平均速度
        relaxation      1.0;
    }
}

BTW，看起来这篇JCP文章不错，CFD界推一下

悬铃神木

@东岳谢谢东岳老师
这个meanVelocityForce的源项我用过，但是和我想要的不太一样，meanVelocityForce也是通过添加一个压力梯度来控制平均速度的，但它给添加的压力梯度项是随时间步不断计算调整的，我想添加一个简单的常数的压力梯度。不过我确实可以通过修改meanVelocityForce来达到这个目的，今后我会试一下这个。
另外，我那个平均速度的代码就是从meanVelocityForce中copy过来的，稍微改了一下下让他能在求解器中运行，现在来看运行的还可以。而且这个平均速度只是为了在log中输出一个当前流场的平均速度，方便我检测求解状况，不会影响迭代求解的，所以还是不太清楚结果中的问题出在了哪里。ORZ

李东岳

我想用q-DNS模拟一个Re_tau=180的槽道湍流,网格与这篇链接文本文献中基本相同。

如果你要实现这个q-DNS模拟槽道湍流，我觉得你可以试试meanVelocityForce，之前我也是用你这种植入代码的方式计算，后来发现meanVelocityForce更简单并且两者效果相同。

这个平均速度只是为了在log中输出一个当前流场的平均速度

我当时植入的代码平均速度是给定的，因为你完全可以不植入任何代码直接用icoFoam做直接模拟，但是速度回往下掉, 因此给定一个固定的平均速度。如果你只是为了输出，那应该没问题吧

悬铃神木

@东岳嗯嗯，我都会尝试一下

悬铃神木

@东岳破案了……
出现错误的原因在于离散格式，当时我看到dnsFoam的那个算例里使用了

div(phi,U)      Gauss cubic;

这个离散格式，一查还是个高阶格式，就直接拿来在我的算例里用了。现在改回Gauss linear格式，算得很好：
替代文字

基本到达了文献中的效果
我翻了一下中文版指南，发现这个cubic格式被描述为dnsFoam专用的

里面的详细原理还不太清楚，我现在对离散格式的选用还理解不深，感觉还是玄学般的东西，哈哈ORZ

李东岳

这个meanVelocityForce的源项我用过，但是和我想要的不太一样，meanVelocityForce也是通过添加一个压力梯度来控制平均速度的，但它给添加的压力梯度项是随时间步不断计算调整的，我想添加一个简单的常数的压力梯度。

你的求解器没有设定平均速度？你的算法是这样的？：

动量预测方程中把pGrad项加入到方程右边，与压力梯度项并列
压力泊松方程中也加入pGrad项带来的影响
考虑pGrad的速度修正

悬铃神木

@东岳是的，求解本身没有用到平均速度，也没有规定平均速度，给它一个压力梯度（实际相当于增加了一个体积力），让摩擦力自己跟压力梯度平衡去，平均速度会在某个值附近上下波动。

李东岳

我试试你这种方法

XieXiaoyang

@李东岳李老师，我看很多文献里，槽道湍流DNS计算时，除了时间平均，还可以做展向和流向的空间平均，在OpenFOAM自带LES Ret=395的算例中，有一个postChannel脚本可以改来用，个人觉得用了这个效果挺好的hhh~

李东岳

@xiexiaoyang 有道理

vbcwl

@李东岳东岳老师您好，我之前了解到meanVelocityForce适合槽道这种几何，然后不可压缩，如果我想做圆环柱计算域的传热，然后采用Boussinesq的话，这种计算域以及轻微的热膨胀还可以使用meanVelocityForce么？

vbcwl

@悬铃神木请问你的rms拟合效果怎么样呢？

学流体的小明

@XieXiaoyang 您好，我想请教一下，像这种 DNS / LES 槽道流的结果，我想画速度剖面，进行正则化时候的摩擦速度${u_{\tau}}$和粘性长度${\delta_{\nu}=\nu/u_{\tau}}$是怎样计算的？
我当前的做法是：使用postChannel（就像channel395那个算例一样）将空间时间都做平均之后，可以得到${u(y)}$这样一个分布，然后计算壁面上的速度曲线的斜率，计算壁面摩擦应力，计算摩擦速度：
\begin{equation}
{u_\tau } = \sqrt {\frac{{{\tau _w}}}{\rho }} {\rm{ = }}\sqrt {\nu \frac{{\partial u}}{{\partial y}}}
\end{equation}
但算出来的摩擦速度和预设的相差很大。所以最后的曲线是这样的
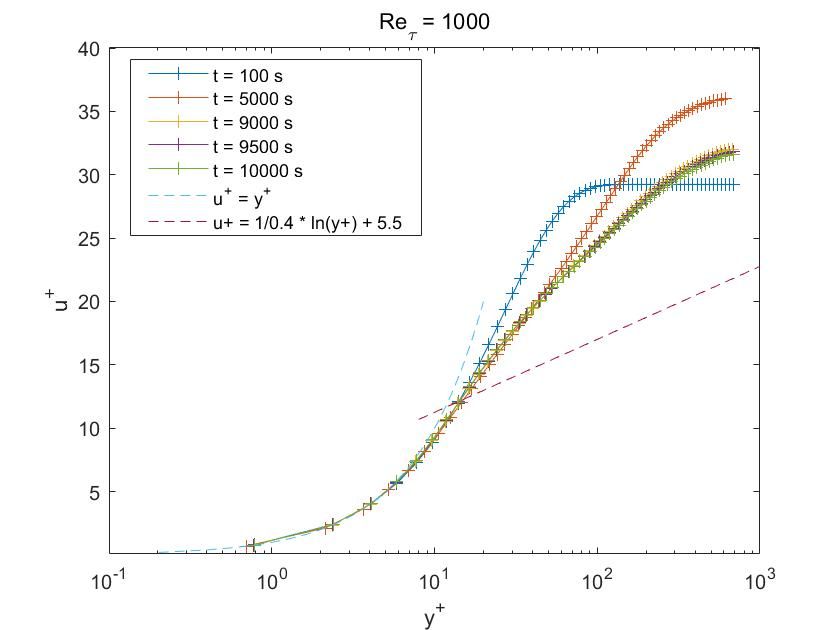
8544ca30-1b5b-4552-9e71-567bb4fe6134-channel1000DirectCalUtao.jpg
算了很久，对数率那里也无法和理论解对上。计算结果的整个曲线也与理论解的形状不符合。
感觉我使用的方法不太对，想请问一下您的做法。

李东岳

你得壁面函数用的哪个壁面函数？标准壁面函数还是Spalding那个

学流体的小明

nut 在壁面上使用壁面函数 nutUSpaldingWallFunction，会出现上面那样的速度分布图
但另外一个${Re_{\tau}}$也等于1000的算例，得到的速度分布也差不多
我等等重开一个帖子说明下问题

SSSSK

@悬铃神木您好，我想请教一下，我也是用了这个工具进行打乱，然后给了一个固定的压力梯度，但他随着时间推移速度还是在不断变小。想问一下您这个也是先变小然后再增大吗？大概算了多久才能和文献对上，压力梯度是给的多少啊

学流体的小明

@SSSSK 建议看下我这个帖子。我自己使用的时候也经常估计不好压力梯度数值和具体的平均速度值，流场速度一直掉，其实就是压力梯度给的动力小于流场的耗散。所以我先用设定平均速度的方法，先让程序算，稳定之后的那个压力梯度就可以知道了。之后再直接用固定压力梯度算。
https://www.cfd-china.com/topic/6248/les直流槽道边界层模拟-如何得到正则化速度u-以及正则化坐标y/3?_=1698989899271

SSSSK

@学流体的小明感谢回复，还有一点我想问的就是固定梯度和固定速度这两个方法最终算出来的结果是一样的吗？如果给定固定梯度我该怎么确定我算的摩擦雷诺数是我想要的那个值呢，是在计算后提取摩擦速度来重新计算然后根据算出来的来调整吗

学流体的小明

@SSSSK
两种方法估计摩擦应力：
第一种是经验公式：
$${{\mathop {\rm Re} \nolimits} _\tau } \approx 0.09 {{\mathop {\rm Re} \nolimits} ^ {0.88}}$$
$${\mathop{\rm Re}\nolimits} = {U_m}\left( {2h} \right)/\nu $$
$h$为槽道半高，$U_m$为槽道平均速度。
第二种是完全发展槽道流中的计算：
$$ \frac{{\partial p}}{{\partial x}} \times h = {\tau _w} $$

CFD中文网

q-DNS计算槽道流遇到了一些问题，求大神们指点